CHAPTER 9
Cosmic Noise
I am embarked on a program to show that there are no general laws that govern—or describe—the physical universe. The laws that we have are either ( 1 ) man-made, as I believe that the conservation laws are, or ( 2 ) like Newton’s laws of motion, they are not fundamental and can be derived from other more fundamental laws, or ( 3 ) they are descriptions of the way that specific things, like electrons and protons, behave. The laws of electromagnetism I believe, fall into this last category. The other laws—Newton’s laws of motion and the conservation laws—can be derived from the laws of electromagnetism. The fact that all these laws can be unified provided scientists like Einstein with encouragement to work for a complete unification of all of our scientific information. But, no one has yet been successful in this enterprise. In my analysis, I have said that general laws imply design. The fact that laws, like Maxwell’s laws, summarize the information contained in a number of other laws does not make them general laws. But, I do have an outstanding problem that requires an explanation if I am to claim that there is no discernible design in the universe—Why are the laws of electromagnetism as mathematically simple as they are? I have never written down these laws for you either in the form of Maxwell’s equations or in the form of the interaction between two charges because, although I say they are mathematically simple, they are far more complicated than Newton’s laws of motion. They are often not even presented in their full form in the first university course in Physics taken by Physics majors. In the simple case of two interacting stationary electric charges, the accelerations depend on the inverse square of the distance between the charges. It is this kind of simplicity that I think must be explained, or it will seem that a designer has been at work.
The order that we find in the physical world, as I see it, stems from the natural recurrences of the three fundamental particles: electrons, protons, and neutrons. Why there are natural recurrences needs explanation but it is not unreasonable that, if we can explain, by a theory of evolution, natural recurrences of plants and animals, the explanation of recurrences of fundamental particles should also be possible.
So far I have ignored gravitational interaction, and I will continue to ignore it for a while. I have ignored nuclear interaction—the interaction between protons and neutrons in the nucleus of an atom. We do not yet have a really clear description of this interaction except to realize that when nucleons—protons and neutrons—are close enough together there is some mechanism which holds them together. The electromagnetic repulsion between protons continues to exist but a different mechanism, superimposed on the repulsion, causes them to be attracted at short-range. This nuclear attraction is the same between proton and proton, neutron and neutron, or proton and neutron. We say it is “charge-independent” meaning that it exists whether the nucleon is electrically charged or not. This seems to indicate that it is a distinct nuclear mechanism which coexists with the electromagnetic interaction. Whatever the nuclear interaction is, the “Law of nuclear interaction” will be of the same type as the “law of electromagnetic interaction” and will be explainable, in the same sort of way, as a description of the behavior of fundamental objects that recur naturally.
Another whole set of facts that I am ignoring, because they seem tentative, are the investigations going on about fundamental particles. This means that I am ignoring all the observed spectrum of particles: the leptons, hadrons, and baryons, as well as the more fanciful quarks, gluons, and so-ons. It is not that I do not think this particle research is extremely important, but I do not believe that we have really settled on any laws. Even if we had, they would again fall into my category of descriptions of specific objects that recur naturally. The simplicities would require an explanation, but that is what many of the attempts to systematize the spectrum of observed particles are concerned with. All sorts of concepts are introduced like “color” and “charm” to try to make it easier to analyze particle physics but, of course, these are man-made.
Perhaps it would be a good idea to record a list of all the laws of physics that I must come to grips within this exploration of mine. F.W. Constant wrote a textbook in 1963 called Fundamental Laws of Physics . Here is his list (Some of the laws have not yet been mentioned):
I. Newton’s law of motion (second).
II. Newton’s law of action and reaction (third).
III. Newton’s law of gravitation.
IV. The conservation of energy principle.
V. The degradation of energy principle (or second law of thermodynamics).
VI. Huygens’ principle of wave propagation.
VII. Coulomb’s law of electrostatic force.
VIII. Ampere’s law of magnetic force.
IX. Faraday’s law of electromagnetic induction.
X. Maxwell’s law of magnetoelectric induction.
XI. The relativity principle.
XII. The quantum principle.
XIII. Pauli’s exclusion principle.
XIV. Conservation of matter principle.
XV. The law(s) of nuclear force. [1]
First of all I must point out again that, to Constant, a fundamental law means something very specific:
The great laws of physics are those that express principles or relations which are independent of the specific properties of certain materials or objects. These laws will therefore be called our fundamental laws; they must be distinguished from those restricted laws which apply only to certain materials and only under a limited range of conditions. By their nature, fundamental laws are not derivable from anything else; they are our starting points in the various branches of physics. [2]
I have been putting forward the thesis that there are no “principles or relations which are independent of the specific properties of certain objects.” My fundamental laws are in fact, the description of the behavior of objects—objects that are fundamental in the sense that the whole universe is composed of these objects.
I will refer in turn now to the different laws in Constant’s list of fundamental laws. I have said that Newton’s laws—if we ignore the law of gravitation—can be explained by referring to the more fundamental laws, the laws of electromagnetism, which Constant separates into the four laws: VII to X. These four are summarized in Maxwell’s laws of electromagnetism, or the laws of interaction between two electric charges. Law IV, the conservation of energy, I have indicated to be only an alternative formulation of other laws. The relativity principle (XI) is partly contained in Newton’s first law of motion which was extended by Einstein to relate to the laws of electromagnetism. I will be writing in detail about this in the chapter called Trapped Inside . The inside referred to is inside the universe. We can only observe the behavior of objects inside the universe and, as I indicated in the chapter on The Impossibility of Isolation , the universe is more than a background for observing behavior. In the present chapter, which I have given the science-fiction style title Cosmic Noise , I want to explore a second facet of the influence of the universe—cosmos—on the fundamental objects.
This investigation will deal first with what Constant calls the “degradation of energy principle (or second law of thermodynamics)” and here the influence of the immediate surroundings on systems of objects—atoms or molecules—is described. Then I will look at the influence of the universe as a whole on the particles, as individuals, and will be coming to terms with part of the information contained in what Constant calls the “quantum principle.” Number XIII, “Pauli’s exclusion principle,” will have to wait until after the next chapter when I discuss The Stochastic Atom .
Just to complete the examination of Constant’s list of fundamental laws, I will mention the others. The one he calls “Huygens’ principle of wave propagation” will be discussed in the chapter on The Two-Slit Mystery . There, I will show that it is information contained in Maxwell’s laws. That leaves the “Conservation of matter principle.” Again, this is not a general law really but a description of the universe—that the numbers of electrons, protons, and neutrons do not seem to change with time. They are extremely durable. I have already hinted at the possibility that this durability may not be a static situation, where a particle just continues to exist in perpetuity, but perhaps a dynamic situation, in which the particle is constantly decaying —disintegrating—and constantly being renewed—rebuilt.
In this chapter, I will concentrate then on “the law of degradation of energy” and “the quantum principle.” For both of these, I will invoke the influence of the environment on a particle or a system of particles. By environment, I mean the rest of the universe, excluding the system of particles itself. It is not usual to pay very much attention to the rest of the universe as far as environment is concerned. Resnick and Halliday say this:
The motion of a given particle is determined by the nature, and arrangement of the other bodies that form its environment. In general, only nearby objects need to be included in the environment, the effects of more distant objects usually being negligible. [3]
This clearly states the position that the effect of distant objects is usually ignored. What Resnick and Halliday call the environment is what we think of as the interacting objects. The effect of any one interacting object decreases as its distance from the particle, whose environment it creates, increases. Since the effect of any one object becomes negligible it is not unreasonable to assume that the effect of the totality of all the objects out there, that form the rest of the universe, is negligible. What I will argue in this chapter is that the effect of all those objects, which of course are made of electrons, protons, and neutrons, is not negligible but is taken into account in four different ways. None of the ways in which the objects out there affect a particular object is directly attributed to those objects by most scientists. I have already discussed the fact that it is those objects that create inertial frames of reference. In this chapter, I will attribute to those objects what is called the degradation of energy principle and the quantum principle; in a later chapter I will indicate that, if the effect of the objects out there is interfered with by some sizable nearby object, the result is an attraction to that nearby object. The nearby massive object casts a shadow, if you will, on the particular object under study and makes the effect of the rest of the objects of the universe asymmetric. That is how I will explain gravity.
Before I launch into a discussion of these different effects, I want to tell you of an incident that happened in 1961. Dr. Donald Ivey and I were asked by the Physical Science Study Committee to make a film titled Universal Gravitation. We wanted in it to show the motion of a planet around a sun graphically, by animation. We were told that this would be possible by using an analog computer at the Lincoln Laboratory of the Massachusetts Institute of Technology. One afternoon we went to the laboratory and were given a demonstration. One spot on the screen of a cathode ray tube was stationary while a second spot was moved about it to represent a planet moving around the sun—or a satellite moving around a planet. The position of the moving spot was calculated, according to Newton’s law of gravitation, using the analog computer. Analog computers were, at that time, much faster machines for making this kind of calculation than digital computers. They could move the spot along reasonably quickly and give a lively display. But, analog computers are not as accurate as digital computers in that they effectively work only to an accuracy of 2 or 3 significant digits—digital computers can operate with six or more significant figures. This meant that the planet’s orbit on the screen of the cathode ray tube did not behave as it should behave according to Newton’s laws of motion and law of gravitation. It should have moved in an elliptic orbit with the sun at one focus and repeated this orbit time after time. What always happened was that the orbit changed its orientation all the time—it precessed. If the same thing had been done using a modern digital computer, the effect would not have been as noticeable, but it would still have been there.
All calculations that we can do on real numbers have, in the end, a limit to their precision and, as time goes on, the orbit would get out of whack . This demonstration made an indelible impression on me. Why doesn’t a real planet get out of whack ? Is there no limit to the accuracy with which nature operates?
The limited precision with which any computer represents real numbers introduces a random element into the results of its calculation. This random element can be made smaller and smaller by using greater precision, but it cannot be eliminated. It occurred to me that this must also be the case with the way the universe operates. There must be an end, a limit to the precision of the operation of laws and, in this limit, there must be a random element operating. Real planets do not behave as our graphical planets did. Why not?
There are two places in physics where random elements are admitted to be present and where the future is not precisely predictable, but is instead probabilistically predictable. These two places are in the second law of thermodynamics and in the quantum principle. But, where does the randomness arise? The laws that we have looked at so far have no such element in them—they are deterministic. If a known situation exists, what happens next is precisely predictable. We say there is a causal connection between the present state and a future state. A law will let you calculate the future state precisely, if you know the present state precisely. And, in fact, the law will tell you precisely what the past states were. Danto and Morgenbesser wrote in their book on the Philosophy of Science :
The initial state is sometimes spoken of as determining every other state of a physical system (it being arbitrary which state we chose as initial)—assuming the system to be isolated. The concept of “isolated system” is difficult to explicate, and many argue that the only instance of an isolated system is the universe itself. [4]
The implication of this is that any departure from deterministic behavior might be attributed to the fact that isolation is impossible. But, we have happily assumed that systems that we were studying, whether they be two particles colliding, many particles colliding, many particles in a cluster breaking up, or two particles in an atom, were able to be isolated or maintained in an environment with which there was no net exchange of energy. Mach indicated that it was essential for progress to focus on part of the whole universe, not on everything at once:
It is certainly fortunate for us, that we can, from time to time, turn aside our eyes from the overpowering unity of the All, and allow them to rest on individual details. But, we should not omit, ultimately to complete and correct our views by a thorough consideration of the things which for the time being we left out of account. [5]
Surely, it is time to consider “the things which for the time being we left out of account.”
We seem to be getting along very well without taking the environment into account. But, to get along we must attribute a probabalistic—random—element to the system under study. David Bohm, in his book Causality and Chance in Modern Physics , suggests that the random influences—contingencies—might better be related to all the rest of the universe:
Every real causal relationship, which necessarily operates in a finite context, has been found to be subject to contingencies arising outside the context in question… For example, in the motion of the planets, contingencies are still quite unimportant for all practical purposes… Now here it may be objected that if one took into account everything in the universe, then the category of contingency would disappear, and all that happens would be seen to follow necessarily and inevitably. [6]
Bohm explains that we resort to probabalistic calculations and speak of randomness and chance because we do not have enough information about all the details of the interaction with the rest of the universe. The events do not really happen by chance—we use chance as a cover for our own ignorance.
In this book, I am trying to maintain that the question of whether the present state of the universe is the result of chance or design—or a combination of chance and design—is an unanswerable question. Most of my effort so far has been spent in trying to show that the evidence for design, through the existence of general laws, is illusory.
Now, in this chapter, the general laws have in them the element of chance. I must show both how the general laws arise and that the element of chance in them is due to ignorance on our part and not due to something in the universe that is inherently random. In this way, they can neither be construed as evidence for design nor for—radical—chance.
I am going to look first at the degradation of energy principle. This is often called the second law of thermodynamics because it appears in the study of heat, which is one of the forms of energy. The law can be stated many different ways, but it is always the same information. Before I say what the law is, I must explain the idea of a closed system. I have shown that if you define different kinds of energy: potential, kinetic, heat, etc., in the right way, energy in an isolated system—sometimes called a closed system—is always conserved. If you calculate the energy at any time by adding up the energy of all the components of the system, you get exactly the same number, no matter how the components of the system interact with each other.
Suppose that the closed system is a large number of atoms of a gas, say helium atoms. To contain such a system we must enclose the atoms in a box—or container. The box must be maintained at a constant temperature, that is so the atoms in the box will have a constant average energy. The temperature of the box must be arranged so that the average energy of the atoms of the gas is the same as the average energy of the atoms of the box, so that there will be no net interchange of energy between the box and the gas contained in it. Then we say the gas in the box is a closed system. Its energy will remain constant with time. The first law of thermodynamics is that in a closed system, energy will remain constant. But, more needs to be said about the behavior in a closed system—energy is not enough to describe what happens. The second law of thermodynamics indicates that there is a direction in which a closed system will change as time goes on; it will not, of itself, change in the opposite direction. We say the process of change is irreversible—it cannot run backward in time. As far as a single interaction between two isolated particles is concerned, everything is reversible. If you saw a movie of two colliding particles run backward, you would not say that it was at all unusual, provided there was no change of mechanical energy into heat. If there is such a change, running the film backwards would look impossible to you. For instance, suppose you took a movie of a ball bouncing on a table where the bounce gradually dies out. Energy is conserved here (first law of thermodynamics) but gradually mechanical energy of the ball —potential and kinetic—changes into heat energy—the ball and the table are warmer. A bouncing ball shows the second law of thermodynamics in action. It is why we believe that macroscopic perpetual motion is impossible. If no energy is fed into the system, all macroscopic mechanical energy gradually is transformed into heat energy.
But, what about a system with no macroscopic mechanical energy, like our gas in a box? What goes on there? The energy is heat energy and stays as heat energy. Is there any direction to processes there? The answer is yes, there is. Suppose you arranged the atoms in the box so that all the faster moving ones were in the left side of the box and all the slower ones in the right side and then photographed the action—if you could. It would not be very long before the atoms were all mixed together with no separation between fast and slow. Showing this movie backward would look ridiculous.
In the actual process the order, namely, separation by velocity—faster atoms at one end, slower at the other—would disappear; disorder would be the final result. This idea can be written many ways. One way is to say that in any natural process order tends to disorder. Another way to record the facts is to notice that if the left end of the box contains faster moving atoms, that end must be at a higher temperature than the right end of the box. After a time the whole box is at the same temperature. We say heat energy flows from the hotter to the colder end. Or put another way, heat does not of itself flow uphill from a colder to a hotter part.
The usual way to justify the second law of thermodynamics is to say that a system that is isolated tends to the state that is most probable—or has the highest probability. Suppose you were playing a game called “locate the atom in a box” by running some wheel of fortune to decide randomly where it should be located and you had atoms, some of which were fast moving and some were slow moving. At each spin, you would place one atom in the box and carry on spinning until all atoms were located. The number of different ways of doing this is enormous, just as the number of different bridge hands that can be dealt is. Many of the ways look the same, sort of jumbled up, disorderly. Only a small number of arrangements would have fast atoms at one end and slow at the other. It is like finding bridge hands with two all red hands and two all black hands. It is very improbable compared to a mixture of black and red in each hand.
So scientists have come to accept the fact that all processes tend to an arrangement that is more probable; and in the end to the one of greatest probability. It is possible, on the basis of probability calculations alone, to predict the actual distribution of velocities of atoms in a gas at equilibrium. The distribution is predictable even though it results from random events. All probability calculations imply randomness, that is, unpredictability which, when you deal with large numbers of things or events, yields virtual predictability. The predictability is not precise predictability but, as the number of individual objects making up the system increases, it might as well, for all the difference it makes, be precise predictability.
So the second law of thermodynamics indicates that there is a randomizing influence on the behavior of systems like gas in a box. Why do we call the law the “principle of degradation of energy.” I have indicated that mechanical energy tends to “disappear” and heat energy “appears”. The second law of thermodynamics tells us also that you cannot transform heat energy back 100% into mechanical energy, although it is perfectly possible to get some mechanical energy from heat. Think of the steam engine running a train. Just as macroscopic perpetual motion is impossible so too is the perfectly efficient conversion from heat to mechanical energy. You always have some heat left, and this is often just wasted in an engine’s exhaust for instance, or given off by a radiator to the air. We think of mechanical energy as first-class energy and heat as second class energy. So the principle of degradation of energy is that all first-class energy naturally degrades into second class energy. We never lose energy, but it becomes less useful to us. What people mean when they tell you to conserve energy is to conserve first-class energy, since, of course, energy is automatically conserved always. It is defined that way. The energy crisis people talk about, is that we are depleting our sources of first-class energy.
To explain the principle of degradation of energy (the second law of thermodynamics) we must either say that there is absolutely no information in it, beyond the laws of interaction of objects (Newton and Maxwell) or to account for the random influences on a system of objects by pointing to the apparently innocent bystander—the box in which the system is contained. Since the box is connected with the rest of the universe, its influence contains the random influences of all the particles in the whole universe. If we could deal with the whole universe, we might not have to worry about these apparently random influences. But, if we try to do this, Bohm says:
Of course, by broadening the context, we may see that what were chance contingencies in the narrower context present the aspect of being the results of necessary causal connections in the broader context. But, then, these necessary causal connections are subject to still newer contingencies, coming from still broader contexts. [7]
We cannot expect to know what it would be like to get outside the universe but what we must do is build up information about what it is like inside.
To me the second law of thermodynamics can be summed up by saying that, although a system can be kept in such a way, relative to the rest of the universe, that there is no gain or loss of energy of the system on the average, it cannot be isolated from the microscopic random influences of the rest of the universe. This means as well that there must always, microscopically, be a give and take of energy between the individual elements of the system and the environment even for what we call an isolated system. The net overall result of this give and take is zero energy flow one way or another—energy is conserved macroscopically. Here is a summary of this in the Physics text that D.G. Ivey and I wrote:
In thinking about gas molecules bouncing around in a container, we know that individually they make collisions with the walls in which they gain or lose energy. However, for a system in thermal equilibrium we assume that on the average there is no net gain or loss, and the total energy of the gas is constant. Therefore, we can think of the collisions with the walls as being perfectly elastic (or think of the walls as being perfectly reflecting) and speak of the gas as isolated, exchanging no energy with its surroundings. It is, however, because the system is not really isolated that the concept of thermal equilibrium exists. [8]
I would say then that microscopic energy conservation is impossible. And this is what I mean by “cosmic noise.” I call it cosmic because the effect is an interaction with the cosmos—the rest of the universe. I call it noise because it appears to the system as a random influence. As Sir Fred Hoyle says:
… by taking account of an influence of the universe, it is possible to avoid the assumption that the local laws of physics are lopsided with respect to time. [9]
We explain the irreversible part of thermodynamics by noting that the effect of the rest of the universe on the system appears to the system as a random influence. I quoted Bridgman as agreeing with this point of view:
What prevents the following out through all future time of a definite sequence is the walls, the atoms of which are supposed to be in such a complex state of motion because they are in connection with the entire outer universe … [10]
The last film that Donald Ivey and I were to make for the PSSC group we called “Energy is not enough.” It was to be a film about the second law of thermodynamics from a microscopic point of view. This view is usually called the statistical mechanics point of view. This is because ideas of probability, or statistics, are applied to the distributions of position, velocity, and energy of atoms or molecules. In the script for the film, we had suggested that the random influence that resulted in the unpredictability of the behavior of individual atoms or molecules had its root in the walls of the container. In the conference with a group of scientists that always preceded the making of any PSSC film, it became clear that no two of those scientists agreed about the basis of statistical mechanics. In the end, the film was never made. I had not before really encountered a situation where it became so obvious that beneath the formulas in science there were so many interpretations. It seems that there is superficial agreement about what we—scientists—all should believe but I found that underneath this is not the case. Kuhn says:
Though there still is a paradigm few practitioners prove to be entirely agreed about what it is. [11]
That brings me to the second fundamental law that I want to talk about in this chapter, what Constant calls the “quantum principle.” I am going to divide this quantum principle into two parts. The whole principle attests to the dual, wave-particle nature of matter and radiation. I will address only the dual nature of matter in this chapter. Radiation’s dual nature I question, and for this reason put it off until the chapter on The Two-Slit Mystery .
Perhaps I should begin by saying where the word quantum comes from. It means a certain amount . Originally, it was applied to electromagnetic radiation. It was decided that the energy in electromagnetic radiation came in certain amounts as a sort of package—a quantum. The amount of energy in a radiation quantum was determined to be proportional to the frequency of the electromagnetic waves. This development took place at the beginning of this century. It was due to the work of Planck and Einstein.
When, in the early 1920’s, there appeared to be indications that the idea of a dual, wave-particle nature could be ascribed to particles of matter, like electrons, protons, and neutrons, the theory that included this property was called quantum mechanics.
Just as the second law of thermodynamics can be stated in several ways, there are several ways of describing what I have called the wave-particle duality of matter. One way was originated in 1923 by Louis de Broglie. He said that there was a wavelength associated with every particle of matter that is moving. This wavelength L was inversely proportional to the momentum m×v of the particle. Thus
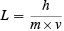
The constant h in this formula was Planck’s constant. It had appeared earlier when Planck and Einstein had said that the energy E in a quantum of electromagnetic radiation—a photon—was proportional to the frequency f of the electromagnetic wave
E = h × f
This is perhaps the most striking evidence of design in the universe—that the constant h, Planck’s constant, should appear in both these formulas and that they both should be so simple. I will have a lot of explaining to do to eliminate proof of a Designer here.
Then, in 1924, the same constant turned up again. This time Werner Heisenberg used it in his uncertainty principle. This principle stated that there was a limit to the accuracy with which the position and velocity of a particle could be measured simultaneously. For a particle constrained to move along a line, the uncertainty in the measurement of position x we call U(x) , the uncertainty in velocity v we call U(v) . The Heisenberg uncertainty relationship for a particle of mass m is
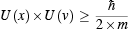
This is a more complicated relationship—or law—than de Broglie’s formula for wavelength. The constant ħ in the formula is not Planck’s constant but is Planck’s constant h divided by 2 times pi. (Remember pi? The area of a circle is pi multiplied by the radius squared.) The uncertainty relation says that the product of the uncertainty in position and the uncertainty in velocity is greater than (>) or equal to (=), ħ divided by two times the mass of the particle.
It can be shown that, although de Broglie’s and Heisenberg’s relations are stated quite differently, they contain the same constant and they really have the same information content. One can be derived from the other. Actually, it is easy—but not really easy—to derive both Heisenberg’s and de Broglie’s relations from a third statement of the same information. If you want to see this done, and are mathematically ready, take a look at Chapter 18 of my textbook Physics (John Wiley and Sons). The actual statement of the relation from which the others can be derived is that the amplitude of the probability density of position for a steady state of a system of particles and the amplitude of the probability density of momentum for that same steady state is that of a Fourier pair (x, k) provided that the momentum is related to k by the relation
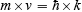
where ħ is, as before, Planck’s constant h divided by 2 times pi.
So there is no need to “explain” all three of these relations —Heisenberg, de Broglie, and the Fourier pair relation. If you explain one, you explain them all.
I am going to suggest that the uncertainty that exists in measuring the position and velocity—or momentum—of a particle (which is really why we say it has a dual nature of wave and particle) is because the motion of a particle has a jitter to it which is the result of the random—uneliminable—influences on it from the rest of the universe. Heisenberg’s relationship has often been presented in terms of the uncertainty in our knowledge of the state—position and velocity—of a particle. Heisenberg has this to say:
Certainly, quantum theory does not contain genuine subjective features; it does not introduce the mind of the physicist as part of the atomic event. But, it starts from the division of the world into the “object” and the rest of the world, and from the fact that at least for the rest of the world we use the classical concepts in our description. This division is arbitrary…[12]
Heisenberg is saying that we want to treat the rest of the universe as classical (deterministically) and this leads us arbitrarily, to assign to the particle itself this uncertainty or dual nature. We say that its behavior can only be calculated probabilistically. But, if we say that there are random influences from outside, the particle is in fact behaving classically (deterministically). Because we can never know all the influences in detail, we are compelled to make probabalistic—or statistical—calculations. Heisenberg speaks about the random influences on the nucleus of an atom which cause it to disintegrate and emit an alpha-particle, apparently at random:
We know the forces in the atomic nucleus that are responsible for the emission of the alpha-particle. But, this knowledge contains the uncertainty which is brought about by the interaction between the nucleus and the rest of the world. If we wanted to know why the alpha-particle was emitted at that particular time we would have to know the microscopic structure of the whole world including ourselves, and that is impossible. [13]
The mechanics that we use to predict what will happen in the nucleus of the atom or in the atom is called quantum mechanics. It is called this because it incorporates the element of uncertainty in the behavior of the particles that constitute the atom. The predictions that can be made using quantum mechanics are probabalistic in nature. There is absolutely no possibility that they can be other than this. Most scientists would say that this is because of the uncertainty principle or because of the dual nature—wave-particle—of all the constituents of the atom. Since I cannot accept the idea of a general law governing—or describing—the behavior of all objects, and that is what either of these implies, without looking for an explanation, I must go further.
I believe that the effect of the universe on each particle is what produces the result that we are noticing here. I believe that the laws of electromagnetism describe accurately how charges would interact if they could be isolated from the random fluctuating influences of the microscopic structure of the universe. Of course, the laws of electromagnetism do in themselves already incorporate the steady part of the influence of the rest of the universe in producing the inertial environment. As Heisenberg says, the division we have now is arbitrary. We assign the randomness to the particles and claim it is part of their nature.
I am going to claim that the behavior of particles is very similar to the behavior of particles of pollen suspended in water which were observed under a microscope in 1827 by the botanist Robert Brown. It was first thought that the random jumpy motions of the pollen particles was due to the fact that they were “alive”. Then it was observed that all tiny particles showed this same kind of motion.
It might have been possible for scientists at the time to say that the particles of pollen, or whatever, had a dual nature or that their behavior was described by an uncertainty principle. But, instead scientists began to attribute their zigzag motion to the influence of their environment. Even though they could not see what was going on, they imagined that the environment was made up of other much smaller particles, moving about in a similar zigzag fashion, bumping into each other and into the pollen particles. The smaller particles were called atoms. Here are Resnick and Halliday:
The earliest and most direct experimental evidence for the reality of atoms was the proof of the atomic kinetic theory provided by the quantitative studies of Brownian motion. [14]
The “atomic kinetic theory” was that atoms in a gas were moving about randomly and bumping into each other and the walls of their container. In doing this, they caused the suspended particles to move about as well. As Resnick and Halliday continue:
The suspended particles are extremely large compared to the molecules of the fluid and are being continually bombarded on all sides by them. If the particles are sufficiently large and the number of molecules is sufficiently great, equal numbers of molecules strike the particle on all sides at each instant. For smaller particles and fewer molecules the number of molecules striking various sides of the particle at any instant, being merely a matter of chance, may not be equal; that is, fluctuations occur. Hence, the particle at each instant suffers an unbalanced force causing it to move this way or that. [15]
For Brownian motion, it has been shown that a relationship of exactly the same form as Heisenberg’s uncertainty relation exists for all Brownian particles.
From the Brownian motion, we concluded that atoms were present. Bohm says:
Thus, in the case of the Brownian motion, the postulate was made that the visible irregular motions of spore particles originated in a deeper but as yet invisible level of atomic motion. [16]
Now we know that an uncertainty relation describes the motion of particles like electrons and protons, which we cannot see. Are we wrong to imagine another invisible level—say of messengers—bombarding the fundamental particles from all sides giving them a Brownian-like motion?
So I turn to cosmic noise to explain the behavior both of systems of particles and now of individual particles.
Summary
1. The natural recurrences of the fundamental particles might be explained by a theory of evolution in much the same way as we explain the natural recurrences of plants and animals.
2. The randomizing influence on a system of particles that is evidenced by the second law of thermodynamics is due to the effect of the atoms in the walls of the container and the entire rest of the universe. The system cannot be isolated from the environment.
3. Microscopic energy conservation is a physical impossibility because isolation of the system is impossible.
4. The behavior of a particle that is described by the uncertainty principle is similar to Brownian motion and is due to the fluctuating influence of the rest of the universe. The fluctuations are describable as random, but the chance element is just an ignorance cover, not radical chance. The randomness cannot, however, be eliminated.
5. Particles have a wave nature only in that their motion, as particles, has a jitter due to the fluctuating effect of the rest of the universe.


