CHAPTER 11
The Two-Slit Mystery
This chapter is called The Two-Slit Mystery . What are the two slits and what is the mystery? The two slits are just that, two slits cut parallel to each other in an opaque screen. They are used to perform the two-slit experiment, an experiment devised by Thomas Young, the early nineteenth century physicist who solved the mystery of the Rosetta stone and disentangled Egyptian hieroglyphics. But, Young left behind him his own mystery, the two-slit mystery.
In the last two chapters, I have been concerned principally with an explanation of the wave-particle duality of matter. In this chapter, I will look at the wave-particle duality of electromagnetic radiation. And that is where the two-slit experiment comes in. It was Niels Bohr who stressed the dual nature of matter and radiation. He spoke about complementarity, saying that the wave and particle aspects of matter were like two sides of a coin. A coin may be seen as either heads or tails but not both at the same time. According to Bohr, the reality of particles like electrons, protons, and neutrons must be described using the complementary models of wave and particle. Perhaps we should refer to them not as particles but as wavicles . This notion of complementarity seemed to Bohr to be very fundamental. As Feuer reports:
When Niels Bohr formulated his principle of complementarity in 1926, he proposed that physicists renounce the hope of achieving a system or theory based on one model, either wave or particle... This duality of complementaries seemed to Bohr "a fundamental feature" in the nature of all human knowledge. [1]
I suppose you might say that he thought that there is ambiguity in nature and our knowledge of it must reflect this uncertainty. This gives rise to the big question of whether this uncertainty is subjective, connected with the state of our understanding of the real world, or objective, as I have suggested. I have attributed the apparent dual nature of particles to the fact that all particles suffer random influences from their environment which are superimposed on whatever influences there are, due to other nearby particles. If there are no other particles nearby we would get completely random motion, much like Brownian motion.
But, my explanation would probably be much too mundane for Bohr. He was greatly influenced by the philosophy of Kierkegaard as presented by Hoffding. This is Feuer's account:
From the proposition that theology is psychology, Kierkegaard (as Hoffding expounded his views) argued that we must simply drop the idea of truth-in-itself, the objective truth; all that we can have is psychological truth, hence subjectivity is truth... Thus were sown the first seeds of the notion that theoretical perspectives on physical experience which seemed contradictory were but complementary standpoints, depending... on the personal decisions of an experimenter, on the particular, experimental arrangement he devised to measure and report on his physical experiences. [2]
This philosophical--or theological--point of view played a profound role in Bohr's vision of physical truth. Bohr's idea was that ultimately, precise knowledge of physical reality was not possible. Always there would be uncertainty. Actually, this particular philosophy comes very close to my own thesis--shades of Kierkegaard perhaps. But, I must try to clarify the difference. Bohr was concerned about whether our knowledge of the universe was subjective or objective. I maintain that we should not be able to tell from our knowledge of the universe whether it arises by chance or by design. If there were laws this would be evidence for design so I believe that there are no general laws, only facts about specific things that recur naturally. The wave-particle nature of all particles of matter looks dangerously like a general law, whether it appears as the Heisenberg uncertainty principle or de Broglie's wave nature of particles, and I must explain it. Heisenberg himself struggles with the subjective-objective nature of these facts concerning uncertainty in his book Physics and Philosophy :
... such a description [of a measuring device] contains all the uncertainties concerning the microscopic structure of the device which we know from thermodynamics, and since the device is connected with the rest of the world, it contains in fact, the uncertainties of the microscopic structure of the whole world. These uncertainties may be called objective insofar as they are simply a consequence of the description in the terms of classical physics and do not depend on any observer. They may be called subjective insofar as they refer to our incomplete knowledge of the world. [3]
In a way, Heisenberg's attitude is not very different from mine when he mentions "the uncertainties of the microscopic structure of the world" as being at the root of the uncertainty in our knowledge. But, the fact is that we do not need to know the details of the influences of the rest of the universe. We assume that they are random and use probability ideas to compute average behavior. We stop concerning ourselves with what we can never know in detail and carry on. And it turns out that it does not really matter. The behavior of atoms, although subject to random influences, is probabilistically predictable. The predictions will never be otherwise--but that is good enough for all our purposes.
The reason that I go into all this wave-particle discussion is that many scientists believe that it is somehow connected with the nature of reality. Reality they believe, is designed that way. Bohr did not say this--he said that it was "a fundamental feature in the nature of human knowledge." If I were to make any statement about "the nature of human knowledge", I would say that it is strictly limited by the fact that we are trapped inside the universe and we must recognize that what we know of the universe cannot be considered to be unaffected by this. Have you ever heard people say that they do not like an "I" novel, where everything that is written is what is known to one person. They feel trapped, limited in what they can know about other characters in the novel. As individuals we are all trapped inside our own bodies and what we know of the universe must come into us, through our senses. We are all trapped inside the universe. We cannot step outside and have a look. We were recently able to step outside the earth--vicariously--and looked back at it--but we can never get outside the universe. Nor can our space ships. Our information is strictly from inside and if you are inside something, it is not a strange idea that the something--the rest of the universe--is affecting the objects you are observing. It would be strange if they were not affected in any way. Classical physics does not take into account the effect of the universe. Bohm says:
This error [uncertainty] arises essentially not because of a lack of knowledge on our part, but rather because of the neglect of objective factors existing outside the context under investigation. [4]
What, I believe, we have done is to assign to the particles themselves a nature that really is the result of influences on them from outside. These influences are basically classical, that is, describable by Maxwell's laws--or Newton's laws. Bohm says:
In physics, the influence of any process on its "background" is even more strikingly brought out by Newton's law that action and reaction are equal. From this law, it follows that it is impossible for any one body to affect another without itself being affected in some measure. Thus, in reality, no perfectly constant background can exist. [5]
Now it is time to move to the wave-particle nature of radiation which to me is a more complicated riddle than the wave-particle nature of matter. Electromagnetic radiation is the name we give to the effect that is produced by an electric charge that is accelerating. The radiation field associated with the acceleration decreases in magnitude inversely as the distance from the source charge to the field point so, at appreciable distances from the source charge, it is the dominant component of the field. If the charge is oscillating, the radiation field oscillates at the same frequency and we say that there are electromagnetic waves. The speed with which the wave pattern travels away from the oscillating charge is the speed with which the electromagnetic interaction travels. The frequency of the oscillation has nothing whatever to do with the speed of travel. We say that electromagnetic waves of all frequencies travel at the same speed, which we call c . The waves travel at speed c because the electromagnetic interaction travels at speed c . If we ask what is travelling in an electromagnetic wave, we should equally well ask what is travelling in any electromagnetic interaction. What additionally is travelling in a wave that is not travelling in any electromagnetic field is a pattern--the wave pattern.
An analogy that might help here is to imagine a hose squirting water out of a nozzle. When the nozzle is held still, the water follows in a certain path. The path would be a straight line if it were not for gravity and wind. If there were no wind it would go in a parabolic path landing on the ground, eventually. If, instead of holding the nozzle still, you moved it back and forth you would see a pattern move out. Each drop of water would move as before in a parabolic path, but a moving wave-like pattern would be formed by the stream.
When the idea of energy conservation was worked out by Poynting for electromagnetic interaction, energy was said to be stored in the field. In a static field, the energy just remains in position but, in a dynamic field which is changing with time, it moves around. It flows outward from an oscillating charge into space. The charge sends energy out. This energy "comes" from whatever is accelerating to produce the waves. All very pretty but, since I say that energy is "all in the mind" and is just an alternative way to describe some of the information in Maxwell's laws, there is no need to ask what carries the energy or whether it is "pure energy" as Weinberg calls it. We can really just forget all about it. Its conservation is assured--it was all defined so that, if Maxwell's laws hold, energy is conserved. But, unfortunately, it gets dragged into a lot of the discussion about electromagnetic radiation. In particular it gets dragged into the particle picture of radiation.
After Maxwell's work, up until the early years of the twentieth century, everyone was convinced that there were such things as electromagnetic waves and that light was simply a range of frequencies of these waves that happen to stimulate our eyes. Our primary source of light is the sun, and we call its light "white light." As Newton had showed, white light can be dispersed into colors, the colors of the rainbow, by letting it pass through a glass prism. This spectrum of colors from the sun is brightest in the green part of the spectrum and tapers off in intensity as you go to the extreme ends of red and violet. The brightness of the green is not just because the eyes are most sensitive to this color, but measuring instruments show that it is really the most intense. The intensity of light, as measured in say energy units, for sunlight has a very typical relationship to color. We know now that the sensation of color that we experience is related to the frequency of the light waves. The violet light has the highest frequency of the waves in the visible spectrum--the red, the lowest. You can plot a graph of energy density against frequency for sunlight, and it is always the same. It is the characteristic mix of frequencies produced by our sun. If we use instruments--not the eye--that are sensitive to all frequencies, we see that the sun produces ultraviolet and infrared radiation as well and the graph of energy density against frequency always shows the results for the full spectrum, not just the visible part of it.
The graph of the sun's radiation can be described by an equation, and this same equation can describe the graphs of radiation from many different hot objects, like furnaces or incandescent light bulbs. We call these bodies black bodies, although you might call them hot bodies. The graphs for all blackbody radiation are describable by the same kind of equation. The equation shows that the radiation depends on the temperature of the hot body. Any hot body at the same temperature as the sun produces white light, with its highest intensity in the green. Cooler bodies peak in the red--they look red hot, not white hot. At lower temperatures, the peak is in the infrared--you can feel the radiation as heat, but you cannot see it. Think of a wood stove.
I tell you all this, which you probably know, because it was in trying to explain the graph for blackbody radiation that Max Planck in 1901 reluctantly offered the suggestion that the oscillators producing the radiation in a hot body change energy by an amount that is proportional to the frequency of the radiation. If the change in energy of an oscillator is E then
E = h × f
where the constant h , multiplying the frequency f , has come to be called Planck's constant. Energy is packaged or quantized. An oscillator's energy does not change continuously but in jumps. Abrupt transitions were not part of classical physics. With Planck, modern physics was born. This is the origin of the quantum theory. Planck said that the energy of an oscillator changed by a quantum, not that the radiation energy was quantized. It was left to Einstein to nail down the quantization of energy in radiation. Feuer notes this:
Einstein was consciously trying to develop a new foundation for physical science; his intent was revolutionary.Whereas Planck was a reluctant revolutionist, unwilling but compelled by the sheer weight of experimental facts to break with the traditional mode of thought... [6]
It is interesting that Einstein was unhappy with the shape of quantum theory--the moment it became connected with probabilistic prediction as it did with Heisenberg. He constantly said, "God does not play dice," to which Bohr is said to have replied "Who are you to tell God what to do." But in 1905 Einstein was young, with revolutionary ideas, questioning everything. He worked on the theory of the photoelectric effect. This effect had been discovered by Hertz when he produced electromagnetic waves, of frequencies lower than the visible, from oscillating electric circuits. Hertz found that light falling on metal surfaces caused electrons to be emitted from the metal--this became known as the photoelectric effect. The effect did not occur, no matter how brilliant the light, unless the frequency was high enough. Einstein said that the amount of energy required to permit the electron to escape had to arrive all at once and could not be dribbled in gradually. He said low frequency light would not produce the effect because the radiation itself was packaged with the energy E in the package being related to the frequency f by the equation
E = h × f
This is Planck's equation, but it now applies to a quantum of radiation rather than to the energy jump of an oscillator. Just as it requires a certain energy to get a rocket away from the earth, it requires a certain energy to get an electron away from the metal. If the radiation energy quantum, called a photon, was large enough it could free the electron from the metal--if the frequency of the radiation were lower than this threshold the electron would not come out. No one low frequency quantum would be big enough, and the effect was not cumulative. Even though you provide lots of quanta below the threshold size, nothing happens. Higher energy quanta than threshold size give the electron a speed when it comes out. Einstein's photoelectric equation is very simple. It is
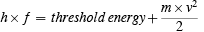
It says: the energy of the incoming quantum h×f is equal to the threshold energy plus the energy of motion of the electron ( m×v2/2 ). This is a statement of energy conservation on the microscopic level. (Remember: the second law of thermodynamics seems, to me, to imply that microscopic energy conservation is impossible due to the random influences of the rest of the universe. But, I leave that for the moment.)
Einstein's explanation of the photoelectric effect convinced people of the quantum nature of electromagnetic radiation, and with it the reality of photons. Planck's work started it but was perhaps too hard to understand. Einstein's 1921 Nobel prize was given for the theory of the photoelectric effect, not for his theory of special relativity. Relativity was hard to understand and seemed "unproved" at the time.
Now it is time to get down to the two-slit mystery. Before Maxwell there was considerable controversy about the nature of light. Newton believed that light was a stream of particles--Christian Huygens, Newton's contemporary, believed that light was a wave. Huygens was Dutch and often observed the ripples in water produced by stones dropping in the canals. If the path of the ripples were obstructed by a barrier, the waves were reflected from the barrier just as light is reflected by a mirror. If the barrier had a hole in it, the waves were obstructed--and reflected--except where the hole was. As the unobstructed part of the wavefront went through the barrier, instead of proceeding like a sort of slice of the original wave pattern, it fanned out, just as if the hole were a new source of waves. This phenomenon is called diffraction, which means spreading out, and is thought to be characteristic of waves. Huygens said that if you could isolate any point on any wavefront, as you do when you obstruct all but a small part, you would find that it acts like a source of wavelets moving out in circles from it. These wavelets, called Huygens' wavelets, do not show in an ordinary wave spreading out because they interfere with one another to produce the overall effect of circular wavefronts moving out from the real source of the waves. If there were two holes in a barrier, the waves emerging from the two holes would interfere with each other and produce an interference pattern.
That brings us to Young and the two slits. Young believed that he could demonstrate that light was a wave by letting it pass through two slits. If it were a wave, each slit would act like a new source of waves just like a hole in the barrier for water waves. The waves from the two slits would interfere with each other, just like the waves from two holes in a barrier for water waves. In certain directions the waves would reinforce and there would be light--in others they would cancel each other and there would be darkness. If you put a second screen up on the side of the opaque slit-screen away from the source, you would see strips of light and dark called interference fringes, parallel to the slits themselves. Young did the experiment, saw the fringes, and settled the argument about the nature of light. It was a wave.
But, if you think of light as a stream of photons as Einstein suggested, what is happening in the two-slit experiment? This is when the trouble starts. Here is an account by Dicke and Wittke in their book Introduction to Quantum Mechanics . They describe the two-slit experiment of Young where the slits are called A and B and the screen where the interference fringes are observed is replaced by an array of photoelectric detectors. They say:
The result is paradoxical in several ways... The photoelectric effect [at the detectors] can be understood only on the basis of the photon picture of light. However, a photon sufficiently small to affect only one electron could presumably not go through both slits A and B. In fact, a photon detector placed at either A or B catches only whole photons or none, never a part of a photon. This raises the question of how a photon which passes through A can be influenced by the presence of B. One obvious possibility is that some photons pass through A and some through B, and that the separate photons act on one another in such a way as to arrive only at the bright fringes on the screen P. This explanation must be incorrect, as can be seen by reducing the intensity of the light to the point where on the average only one photon per minute passes through the system. Even in this case the photons continue to arrive at only the bright fringes!
One striking thing about this experiment is that the behavior of any given photon is largely unpredictable... The intensity distribution over a fringe merely serves to give a probability distribution for the arrival of any given photon; it does not allow an exact prediction of where the photoelectron will appear... If either slit A or B is closed, photons begin to arrive at locations where there were previously dark fringes: a decrease in the number of paths by which a photon can get from S [the source] has resulted in an increased probability [of arrival]. [7]
You can see that it certainly is not simple. Here is Heisenberg himself on exactly the same theme, this time with a photographic plate as a detector:
If one describes this experiment in terms of the wave picture, one says that the primary wave penetrates through the two holes; there will be secondary spherical waves starting from the holes that interfere with one another, and the interference will produce a pattern of varying intensity on the photographic plate.
The blackening of the photographic plate is a quantum process, a chemical reaction produced by single light quanta. Therefore, it must also be possible to describe the experiment in terms of light quanta. If it would be permissible to say what happens to the single light quantum between its emission from the light source and its absorption in the photographic plate, one could argue as follows: The single light quantum can come through the first hole or the second one. [8]
One way often used to get around this perplexing problem is to say that the photon picture of radiation applies only to the emission process, as Bohr claimed, and to the absorption process, as Einstein claimed, and has no validity in between. What happens during the transmission remains a mystery. Not very satisfactory as far as I am concerned. I can remember when I first studied interference, wrestling with light's dual wave-particle nature--I could not reconcile the duality no matter how I tried. It all seemed like double-talk. Many scientists welcome the mysterious--it makes science more fascinating. It makes me uneasy. I always feel that I have somehow just been stupid in not getting the point.
Huygens' principle is used to explain the behavior of light waves at a barrier. But, where did Huygens' principle come from? From the observation of water waves? It should be possible to derive it from Maxwell's laws of electromagnetism. Maxwell's laws are consistent with an alternative formulation which focuses on the electromagnetic interaction between charges. In this alternative formulation, it is clear that all electric effects travel at speed c and in straight lines. How can light be diffracted if it comes to an opaque screen with a slit in it? It seems to go through the slit and then spread out--some light seems to go straight through--some changes direction. This is completely inconsistent with Maxwell's laws. The same things could be said about the refraction of light as it passes through a prism. Its direction is changed. How can this be consistent with the idea that light travels in straight lines? Most scientists will say that light travels more slowly in a medium like glass and this is why it changes direction. Different frequencies of light travel at different speeds in a medium. This is why light is spread out in a spectrum by a prism--different frequencies are refracted different amounts. We call it the dispersion of light into a spectrum. What about diffraction? The explanation you often get is that light changes direction at a narrow opening because it is a wave, and waves bend around corners.
For many years, I had always happily used Huygens' principle to "understand" the behavior of light waves in a medium and passing through small openings and never questioned what was necessary to justify such a principle. The apparent slowing down of light in a medium, other than vacuum--or air which is not very far from a vacuum compared to solids like glass, or liquids like water--can be explained by considering that the atoms of the medium are caused to produce secondary electromagnetic waves by the incoming waves. The total electromagnetic field in the medium is the result of the superposition of the incoming field and the secondary waves produced by the atoms of the medium. These secondary waves have the same frequencies as the incoming waves but are not exactly in phase with them. The net result is the illusion that the wave is travelling more slowly in the medium. It is an illusion however since each wave that interferes to produce the resultant wave is actually travelling at the speed c. The incoming wave continues through the medium at speed c and superimposed on it are waves from the atoms of the medium, all of which travel at speed c . They all add up, by superposition, to a resultant wave that seems to be traveling more slowly than speed c . Very tricky! What is more, the resultant wave can be in a different direction from the incoming wave, depending on how the incoming wave is oriented to the interface between the air and the medium. This is the refraction or bending that we observe. No wave is actually bent. The incoming wave keeps right on going. The secondary waves from the atoms of the medium move straight out in all directions from their source atoms. You will recall that one of our basic facts about electromagnetic interaction is that different fields superimpose but do not interfere with each other. What we call the interference of waves really should be called the superposition of waves.
What about diffraction--do waves bend then? Of course not. The wave that comes up to the screen goes right through the screen. As it does, it sets the atoms in the screen oscillating so that each is a source of secondary waves. There are no secondary waves along where a slit is. The resultant of all these waves superimposed is exactly the same as if there were no incoming wave or secondary sources in the screen but instead a series of secondary sources where the slits are. It is an illusion but a completely convincing one.
The simple mathematical argument for this is not very difficult to understand. Imagine an opaque screen with two slits cut out, but instead of throwing away the parts that you cut out you leave them in the openings. So the screen really has no holes in it. I will call the hole fillers "plugs". On the shadow side of the screen the total electric field E is zero--there is no light. Remember--it is an opaque screen. But, this field is the sum of the fields of the light source E(source) and the field due to the atoms in the screen E(screen). This latter field is the sum of two parts, the field of the screen with slits E(slit-screen) and the field of the plugs E(plugs). So we can write the equation
E (source) + E (slit-screen) + E (plugs) = 0
The electric field on the shadow side with the source and plugged screen in place is zero. The fields of the source and screen are superimposed and canceled exactly. Now what is the field when we remove the plugs from the holes? It is
E (source) + E (slit-screen)
But we know by looking at the other equation that this must be
-E (plugs)
The field on the shadow side is the same size as if there were just oscillating charges in the plugs. The intensity of light depends on the square of the field so the minus sign does not matter.
So Huygens' principle, which says that the wavefront across the slit opening acts like a series of secondary sources, is right because it is exactly the opposite of what is there, that is, secondary sources all along the screen everywhere but at the opening.
It makes quite a difference to your view of what is happening when you realize that a principle works because it is completely wrong, as far as light is concerned. Light waves do not ever really change speed or direction. If they appear to, it is always an illusion produced by a cooperative effect of many atoms. I found this interpretation quite shattering when I first read it. It is like hearing that black is white. I am sure that it opened my eyes to the possibility that other ideas I accepted might be exactly opposite to what I had been told.
If we go back now to the photon picture, where does that leave us? L.I. Schiff in his book on Quantum Mechanics addresses the problem:
From the point of view of the particle picture [of light], we may then ask how it is that a stream of independent photons, each of which presumably can go through only one of the slits, can produce a diffraction pattern that appears only when both slits are open... In this question is implicit the assumption that the photon actually does go through a particular one of the two slits. [9]
The waves that produce the effect go right through the whole screen including the slits and secondary waves are produced by the atoms in the screen. It is difficult to see how a single incoming photon can produce the effect. It really must spread out over the whole screen and interact with all the atoms. The two-slit mystery gets much worse. But after all this trickery and illusion, perhaps the existence of photons is an illusion. Perhaps it is useful because it is exactly wrong. There are scientists who believe in a semiclassical quantum theory. They believe that light is a wave only and that particles of matter give rise to the peculiarity we label uncertainty. These semiclassical theory (SCT) people say that the reason photons can be successfully used to describe the emission and absorption of energy is because the matter does not behave classically. This is basically my position--I would say because microscopic energy conservation is impossible. Semiclassical theory has actually been successful in explaining the photoelectric effect although I cannot give the argument here. It is rather a shock again to learn that the photoelectric effect which is supposed to have proved that photons exist can be explained without any reference to them whatsoever. In SCT it is assumed that quantum mechanics describes the behavior of atoms and that light is adequately described as a wave. Most of the arguments about the need to have radiation quantized involve the assumption that, in microscopic processes, energy is conserved. This is, from my point of view, a weakness since I believe that microscopic energy conservation cannot be a fact because of the impossibility of isolating the system from the random influences of the rest of the universe.
It is very easy to confuse the statements "that Einstein's theory of the photoelectric effect proved the existence of photons" and "that scientists became convinced about the reality of photons by Einstein's arguments concerning the photoelectric effect." Semiclassical theory explains the photoelectric effect without any reference to the idea of photons or to the idea of microscopic energy conservation. Does this mean that we can dispense with photons? Not quite so fast! What about Bohr's relation for the frequency spectrum of hydrogen? His relation is
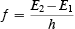
If it is rewritten as
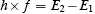
it becomes a statement of microscopic energy conservation. The energy of the photon emitted by the atom h×f is equal to the difference between the initial energy state of the atom E2 and the final energy state of the atom E1 . Again, we find the two ideas coupled--photons and microscopic energy conservation. But, Bohr's relation too can be derived without any reference to either photons or energy conservation, using semiclassical theory. What you use is Schrödinger's equation for the atom and Maxwell's equations for the electromagnetic waves.
My idea that microscopic energy conservation is not true can actually be argued from Schrödinger's equation. Rather than speaking about the hydrogen atom I will refer to the linear harmonic oscillator. In a classical oscillator, like a pendulum bob swinging back and forth, the energy of the oscillator depends on the amplitude of the swing. If the swing is bigger, the energy is bigger. A classical oscillator can be stationary and have zero energy. A quantum oscillator cannot be stationary. A quantum oscillator of frequency f has, as its lowest energy, the energy
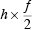
This is called the zero-point energy of the oscillator because if a group of quantum oscillators could be cooled to a temperature of absolute zero, where all motion is supposed to cease, they would still each have this energy. In the Brownian motion picture of quantum mechanics the oscillators would still be in motion--Brownian motion is a perpetual motion. (Of course it is not a macroscopic perpetual motion.)
If you examined the probability distribution function for the quantum oscillator in its ground state you would find that the probability of the particle in the oscillator being at the equilibrium position, at the center of its oscillation, would be the highest and then it would taper off on both sides of the equilibrium position. If a classical oscillator had an energy of h×f/2 there would be a limit to how far away from equilibrium the particle would get. The probability of the quantum particle being outside this classical limit, as determined by solving Schrödinger's equation for the harmonic oscillator, is not zero, even though it tapers off rapidly outside the classical limit. But, how can energy of position be larger than the total energy, which it must be if the particle is outside the classical limits of oscillation? Certainly, the energy of motion cannot be negative. The energy of the oscillator must in fact be greater than the average energy h×f/2 whenever it is outside the classical limit. Many say that there is an uncertainty relation between energy and time that is similar to the one between position and velocity. They argue that the particle can have an energy larger than permitted by energy conservation, but only for a limited time. This sounds to me suspiciously like saying that, on the average, energy is conserved, but energy is not conserved microscopically. The microscopic system, the quantum oscillator, has an average energy of h×f/2 but from time to time has more or less energy. Energy is not constant in a microsystem.
If we accept as a basic premise that, in reality, microscopic energy is not conserved then the picture, begun by Bohr and taken directly into quantum mechanics, that his frequency relation describes an electron jump is a lot of nonsense. The Bohr condition is a clear statement of energy conservation in a microsystem. You can't have it both ways. So I reject Bohr's interpretation. I reject quantum jumps, and I reject photons. Thismeans I reject the particle picture of electromagnetic radiation.
Let me summarize all this. Although I reject a particle picture of radiation, I affirm a particle picture of matter. If an electron is really a particle, the probability amplitude for it in the stable excited states in an atom or an oscillator cannot be right. Recall that I said that each of these has nodes, places where the probability becomes zero. The probability amplitude is non-zero on either side of each node. So the particle, if it is a particle and cannot disappear and reappear like a Cheshire cat, cannot be in such a state. It can be in a ground state because that has no nodes. But, we know that the frequencies in the hydrogen spectrum are related to the average energies associated with the stable excited states as described by the Bohr frequency condition. How can this be reconciled with a view that the stable excited states are exactly those states where the electron cannot be?
Mathematically the wave function for any dynamic state of the quantum system can be described as a combination of the wave functions for the stable excited states. But, I would say that no pure stable excited state is possible. The electromagnetic radiation produced by an atom then will be related to the energies associated with the stable excited states exactly according to Bohr's relation, but the system cannot ever be in any of these states. It is a situation just like Huygens' principle--Bohr's relation is right because it is exactly wrong. Bohr said the particle can only be in one or other of the set of stable excited states that are proper solutions of Schrödinger's equation. I say these stable excited states are all improper in that they contain nodes which means that, unless the particle is an escape artist, it cannot exist in such a state.
I tried to simulate the Brownian-motion atom on the computer, you may remember, and found no excited stable states. In fact, my atom kept expanding. How do you prevent this? In terms of energy, you need to radiate some energy all the time. In equilibrium you should radiate just as much as is coming in from the rest of the universe to keep the Brownian motion going. And that must be what happens if there is such Brownian motion of the electron in the atom. It must be radiating all the time because it is being accelerated all the time. In the ground state it radiates a continuous spectrum. In any disturbed condition which you get if you give it extra energy, it radiates discrete frequencies, as given by the Bohr relation, as well as a continuous spectrum of frequencies due to the continuing Brownian motion.
The radiation from atoms even in the ground state could be exactly what is producing the Brownian motion in other atoms. And that brings me to the other cornerstone of the dual picture of radiation--Planck's blackbody radiation equation. Many believe that Planck's blackbody radiation proves the need for quantized energy states in atoms. It has been shown by Boyer and Theimer that Planck's equation could be derived instead by assuming a zero-point energy of h×f/2 . It is clear from what I say where this would come from. Theimer says:
Some fascinating new ideas concerning the physical meaning of the quantum theory have been developed in a series of papers by Boyer and a related paper by Nelson. In Boyer's work the main new concept is the existence, at the absolute zero of temperature, of a classical fluctuating, electromagnetic background radiation which is, in some unknown fashion, equivalent to the ground state of the radiation field in quantum electrodynamics. Boyer demonstrates that incorporating this radiation background into classical statistical physics makes possible a classical derivation of Planck's blackbody spectrum. He also suggests that the universal background radiation might be the source of the random perturbations, postulated by Nelson, which transform continuous classical particle motion into an equivalent random-walk [Brownian] process.
He continues:
What is the origin of the zero-point radiation? ... The zero-point radiation is a self-consistent radiation field in dynamical equilibrium with all the electrically charged particles in the universe. These particles perform a complicated Brownian motion, in the spirit of Nelson's work, which is caused by random absorption and emission of the self-consistent zero-point radiation. And this radiation has such an energy density that there is no net time-averaged energy exchange between matter and radiation at the absolute zero of temperature. [10]
So the continuous radiation spectrum from atoms that I believe exists even in the ground state is not just hiding in the blackbody radiation--it is necessary in order to give it the distribution that it has. This makes Planck's notion of quantized energy transitions for oscillators as an explanation of blackbody radiation unnecessary.
In this chapter I have been looking at the great difficulty that I have encountered over the years with the dual, wave-particle picture of electromagnetic radiation. In my undergraduate education a wave picture was always used to explain the reflection, refraction, and diffraction of light. Young's double-slit experiment on the diffraction of light by a screen with two slits was offered as conclusive proof that light was a wave. You have seen from my quotations what a tangle various physicists get into when they try to understand the two-slit experiment in terms of the particle, or photon, picture of light. Most of these explanations refer to the photon passing from source to screen by way of one or other of the two slits.
But, the present wave view of the two-slit experiment--which many physicists are unaware of--is that the source waves pass right through both the screen and the slits. These source waves have superimposed on them waves from the atoms in the screen that are forced to vibrate in sympathy with the source waves passing through. The net result of all these waves, as they superimpose--or interfere --is a pattern of light and dark fringes. As it happens, there are just as many waves of light passing through a dark fringe as a light fringe, only at a dark fringe they are out of phase and cancel, at a bright fringe they are in phase and add.
It is important to notice that light does not appear to be diffracted unless there are a lot of sources present--the primary source and the secondary sources in the screen. Light always travels in straight lines from its source to the point of observation. It is an illusion that light goes from the source to a slit and then changes direction as it proceeds to land on a bright spot on the screen.
To me it is a contradiction to say that a single photon interacts with many atoms in the slit screen--especially when you say that a single photon, at least, is necessary to trigger a detector in the second screen. (This latter is held to be true whether the detector is an atom of a photographic plate or a photoelectric detector.)
You probably have heard it said that light travels in straight lines unless it passes through a narrow opening in which case it is bent or changes direction. This bending is an illusion provided by the presence of matter in the electromagnetic field of the primary source of the waves.
Exactly the same situation holds for refraction. You probably have heard that light travels at speed c in a vacuum but, in a medium, it travels at a lower speed. This "explains" how it changes direction--is bent or refracted--as it enters a glass prism. But, this is also an illusion. The superposition of the primary source waves and the waves from the atoms in the glass give the illusion of a wave slowing down as it enters the glass and changing direction. When a prism produces a spectrum of light, it is foolish to imagine a red photon being emitted from the source, travelling at speed c until it reaches the surface of the prism then slowing down and changing direction in the glass and finally emerging, speeding up, changing direction again and landing on a spot where the red of the spectrum is. The photon picture is absolutely inconsistent with the wave picture.
When I was young, I often asked my Mother how a magician had done a certain trick. My Mother's stock answer was "It's all done by mirrors." When you have an object, say a candle, in front of a mirror there is an illusion created that there is a second candle, the image, behind the mirror. If the object candle is hidden from your view, you might believe that the image candle was a real object. No doubt, many magic illusions do involve the use of mirrors. But, the explanation you usually get about the reflection of light by a mirror is really an illusion. Light from the candle we say goes up to the mirror and is bounced off--reflected--to your eye. It then seems--if we assume light always travels in straight lines--to be coming from behind the mirror, from the image. But, the bouncing is an illusion. Light from the object candle passes right through the mirror. In the mirror, secondary sources, excited by the incoming light, radiate what comes out in front of the mirror, superimposing to seem like waves from the image. The light from the secondary sources that goes behind the mirror cancels the waves from the primary source and there is the illusion of darkness. But, remember--there are many light waves behind the mirror.
In this book, I have been looking for explanations of physical laws. I cannot be satisfied with answers that tell me "It's all done by mirrors." Wave-particle duality of radiation is such an answer.
Summary
1. Semiclassical theory treats electromagnetic radiation as a wave, and it treats particles of matter as described by the uncertainty principle--meaning to most that particles have a wave nature. The photoelectric effect and Bohr's frequency relation can be explained by semiclassical theory. I accept a wave theory of radiation and a particle theory of matter. For me, the wave nature of a particle is due to the random fluctuations in its motion.
2. The energy distribution in blackbody radiation can be explained on the assumption that atoms radiate even in the ground state, rather than that there are quantized excited states. Quantization of energy in radiation is, I believe, not necessary to the explanation of any phenomenon.


