CHAPTER 8
The Energy Crisis
Newton's studies of the way that objects interact with each other showed that the ratio of the accelerations of the interacting objects was a constant, independent of the distance between them and their velocities at the time of their interaction. In the last chapter, I described the interaction between electric charges and indicated that this interaction does not fit the Newtonian idea of interaction. Because the interaction is not instantaneous, whenever there is a relative motion of the interacting charges, the effect is complicated. In an attempt to try to simplify the calculation about what happens, we introduce the idea of an electromagnetic field. At any time the field at particle number one--if you call the interacting particles "one" and "two"--is due to particle number two's position and motion--velocity and acceleration--at an earlier time, called the retarded time. The position of particle two at the retarded time is called the retarded position. The duration of the retardation is the time required for the electromagnetic effect to travel in a straight line from particle two, at its retarded position, to particle one in its present position. The speed of electromagnetic interaction is a constant--we name it c . Its value, as I said before, is 186,000 miles per second which is 3 hundred million meters per second. This is an extremely high speed, and you can see that, unless particle two is moving fairly rapidly, it will not have moved very far from the retarded position in the interval between the retarded time and the present.
It is very difficult to think about the interaction between charged particles and not think, as Maxwell did, that there must be something travelling from particle number two to particle number one--and, of course, vice versa. This something I have called "messengers" although I have not yet made any attempt to quantify this messenger model of electromagnetic interaction. One of the reasons for putting this off is because there is a competitor for what is travelling in electromagnetic interaction and that competitor is called "energy". I have entitled this chapter The Energy Crisis because, if I am to make any serious progress with a messenger model, I must first dispose of the energy model.
Energy started as a concept, like force or field, which helps make calculations about the behavior of interacting particles simpler. But it has, by degrees, been invested with more and more significance until now it has become to many people not only a part of nature, a reality, but, to many, the very basis of all reality. As an example of the most extreme reification--if not deification--of energy I quote Werner Heisenberg:
Energy is in fact the substance from which all elementary particles, all atoms and therefore all things are made, and energy is that which moves. Energy is a substance, since its total amount does not change, and the elementary particles can actually be made from this substance as is seen in many experiments on the creation of elementary particles. Energy can be changed into motion, into heat, into light and into tension. Energy may be called the fundamental cause for all change in the world. [1]
I quote this to show you just how far very respectable physicists get carried away in their regard for energy. If it is not energy itself that grips scientists, it is usually the general law called the "law of conservation of energy." I will outline how this law fits in with Newtonian interaction and electromagnetic interaction in turn so that you can appreciate just what it is about, but first I quote a typical enthusiast for the law - Professor R.P. Feynman:
There is a fact, or if you wish, a law, governing all natural phenomena that are known to date. There is no known exception to this law--it is exact as far as we know. The law is called the conservation of energy. It states that there is a certain quantity, which we call energy, that does not change in the manifold changes which nature undergoes... It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number and when we finish watching nature go through her tricks and calculate the number again, it is the same. [2]
To Feynman, the law of conservation of energy is a fundamental part of nature's bag of tricks. It is to him part of the grand design, one of the rules of the game, perhaps the most basic rule since it "governs all natural phenomena that are known to date."
The law of conservation of energy, and with it the concept of energy itself, must be attacked directly if the notion that the existence of laws governing--or describing--the physical world is to be believed to be an illusion. The metaphysical power of any conservation law is very great. Here is Mach:
... the notions of the constancy of the quantity of matter, of the constancy of the quantity of motion, of the indestructibility of work or energy, conceptions which completely dominate modern physics, all arose under the influence of theological ideas. [3]
As Mach says, constancy within change is a deeply rooted theological idea. Do you know the famous hymn "Abide with me"?
Change and decay
In all around I see
Oh Thou who changest not
Abide with me.
Not only is the unchanging element within a constantly changing environment important to us theologically, it is important to every accountant. Books must balance--if something disappears, it must be explained. Whether it is our orderly accountant's attitude in science or a deep-seated yearning for the eternal, somehow the law of conservation of energy has cast its spell over us and we see it as general and fundamental.
Where did it all start? It started with what is known as the work-energy theorem. This is really a restatement of the definition of velocity and acceleration combined with Newton's second law of motion. I will show you what it is. Suppose that an object is moving along in a straight line with constant acceleration a . This means its velocity is changing uniformly with time. Suppose that it starts at time zero with a velocity zero--from rest as they say. As time goes on, its velocity will increase. At a later time t its velocity v will be v = a × t . This is the definition of constant acceleration. In time t it will travel a certain distance d. If it were travelling at constant velocity v , it would travel a distance d = v × t --that is the definition of constant velocity v . In the accelerated case, the velocity is not constant but changes from 0 to v . The distance travelled will be d = (average velocity) × t . The average velocity will be v/2 . So d = v × t /2 . Using the value for the time of the trip from the other equation v = a × t , or t = v /a , we get
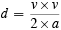
We can rewrite this equation as
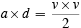
or
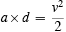
If the acceleration is varying, we multiply the instantaneous acceleration by the small distance travelled when the acceleration has that value and add this up over the whole trip. The right-hand side of the equation stays the same. I will just stick with the constant acceleration case because all that adding up of little pieces involves calculus.
Now comes the time to stir in Newton's second law of motion which is
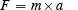
I do not write arrows over F and a here because they are both along the straight line where the motion is taking place. From this equation and the previous one we get
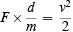
or
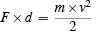
Now we are ready for the work-energy theorem. We define a new concept "work" which is the force exerted multiplied by the distance over which it is exerted. So here by definition
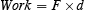
We then define a second quantity which we call the "energy" of the moving object which is its mass multiplied by its velocity squared all divided by two.
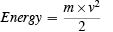
Having defined these two quantities, we now see that our equation says that the work done--by exerting a force over a distance--is equal to the energy of the object that has been accelerated. Sometimes the energy of the moving object is called energy of motion or kinetic energy.
We have introduced--defined--two new concepts: work done by a force and energy of motion. We say, as if these concepts had some existence independent of these definitions, that if you do work on an object, its energy increases. This has no more information than Newton's law has, namely, that if you act on an object with a force, it will be accelerated. This is well understood by all scientists. Here is a quote from a university physics textbook by Resnick and Halliday:
The work-energy theorem does not represent a new, independent law of classical mechanics. We have simply defined work and kinetic energy and derived the relation between them from Newton's second law. The work-energy theorem is useful, however, for solving problems in which the work done is easily computed and in which we are interested in finding the particle's speed at certain positions. [4]
The principal use of this new law is to make calculations about the speed--velocity--of an object that has been subjected to a force where we can make the calculation of the work easily. A force is exerted only if our object is near another object or, as we say, is in the field--of influence--of the other object. According to Newtonian mechanics, if an object is at a certain position in the field of another object and released, it will move in an accelerated manner either towards the object, or away from the object, depending on what the two objects are. If they are both electrons, they will move apart. If one is an electron and one a proton, they will move together.
For certain kinds of fields, called conservative fields, the work done by the force on an object released at one point A in the field and moving to another point B is independent of the particular path that the object takes from A to B. The work done can then be expressed as the difference between two quantities that depend only on the positions of the two points A and B in the field. If we call these two quantities potential energy, then the work done on a moving particle which travels from A to B is just
(Potential Energy at A) - (Potential Energy at B)
This is the definition of the term potential energy (P.E.). Now if we go back to the work-energy theorem we see that, if the object starts from rest at A and is accelerated to B where it has a speed v , then
(K.E. at B) = (P.E. at A) - (P.E. at B)
Since the Kinetic Energy (K.E.), as defined, is zero at A (where v = 0 ), we can write
(K.E. at B) - (K.E. at A) = (P.E. at A) - (P.E. at B)
or regrouping the terms in the equation
(K.E. at B) + (P.E. at B) = (K.E. at A) + (P.E. at A)
This is the first appearance of the idea of energy conservation. If we say that the total energy of the object is the sum of the potential energy and the kinetic energy then this equation says that
(Total Energy of object at B) = (Total Energy of object at A)
The energy of the object is conserved, and this is the law of conservation of energy. As an object moves in a conservative field, there is a quantity --Feynman calls it "a number"--which we have named energy which does not change. We say it is an invariant of the motion. How wonderful nature is! Descartes is quoted by Mach as saying:
Therefore, it is wholly rational to assume that God since in the creation of matter he imparted different motions to its parts, and preserves all matter in the same way and condition in which he created it, so he similarly preserves in it the same quantity of motion [sometimes energy]. [5]
Having gone to the trouble of defining all these new concepts: work, kinetic energy, potential energy, total energy, in order to disguise Newton's law of motion, we stand back and pronounce it as part of the grand design.
I said that it is only for certain Newtonian type interactions that this law of conservation of energy holds. These include gravitation and electrostatic interactions and actions of this sort that happen in isolation of other nearby objects. These must of course be the limitations, since conservation of energy is really Newton's second law in disguise. Perhaps I should say that the same facts about interaction can be expressed in different "guises"--but the information content is the same in each guise.
I have said that the conservation law idea is very gripping. You begin to believe that energy is something that really exists. Gradually you are led to believe that an object can possess certain kinds of energy and that the total amount that it possesses does not change. This is the way we analyze what happens when an object moves in the field of another object which itself remains fixed. What happens when both interacting objects can move? How do we analyze the situation then? Suppose object number one is moving at speed v directly toward object number two, initially at rest, and that the two objects repel one another. Suppose also that the two objects are identical. In the interaction, we know, using Newton's third law, that the forces are equal and opposite at all times. This does not immediately mean that the energy lost by one object is equal to the energy gained by the other since the equal forces may be exerted over different distances. We do know that they are exerted for the same length of time--the time for the interaction to take place. So we define a new quantity called "impulse" which is the product of force multiplied by the time over which the force is exerted. If a constant force F is exerted on an object for time t , the impulse is F × t. Using Newton's second law this is m × a × t. But, if the body changes from a velocity 0 to a velocity v under the influence of the constant force, v= a × t , so that the impulse is equal to m × v which we call the "momentum" of the object. Just as we had the work-energy theorem, we now have the impulse-momentum theorem. The impulse given to an object equals the momentum of the object.
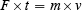
One of the big differences between the two theorems is that work and energy are just numbers that have a certain size--the numbers may be positive or negative. But, impulse and momentum are quantities that have both size and direction.
Using Newton's third law we can show that, if two objects interact, the change in momentum of one object is equal in size and opposite in direction to the change in momentum of the other. This means that the total change in momentum is zero. Momentum is conserved in an interaction. This is called the law of conservation of momentum and is a direct consequence of Newton's laws of motion. It is not new information. It is necessary to use both conservation laws to analyse an interaction since between them they give the same information as contained in both Newton's laws of motion.
Using the conservation laws you can tell that if two identical objects--balls--collide by having one start at rest and the other comes toward it with a speed v that after collision the speeds will be reversed. If each has a mass m , before collision the energy is m × v2 /2 . The potential energy is zero both before and after collision because the objects are assumed to start and finish out of range of any interaction. This means that the only energy before and after is kinetic energy. It seems that the energy of the system is passed from the incoming ball to the outgoing ball during the collision. As far as momentum is concerned, before collision it is m×v+0 --after collision it is 0+m×v . Both velocities are in the same direction so momentum is also conserved. Momentum is passed from the incoming ball to the outgoing ball.
Neither momentum nor kinetic energy are quantities that are independent of the frame of reference that you use for observing the collision. Suppose you imagine the collision between the two identical objects from a frame of reference that is moving along with the incoming object at a speed v relative to the first frame we spoke about. In this moving frame, the incoming object from frame one would seem to be at rest. But, the object that was at rest in frame one would be moving towards the first object with a speed v. The whole collision would seem to be the other way around. If you think of energy--in frame one the kinetic energy of object one is passed over on collision to object two--in frame two the kinetic energy of object two is passed over on collision to object one. How can energy as we have described it be anything real when, depending on our frame of reference, it is passed in opposite directions? And one frame is as good as another for viewing the event. They are both inertial frames, and inertial frames are equivalent.
The same remarks can be made about momentum although, strangely enough, no one seems to speak of momentum as a thing. Perhaps the reason is that we introduce a great many properties all called energy, the sum of which remains constant in an interaction. I have already spoken about kinetic energy and potential energy but there are more. Another is heat energy. Kinetic energy shows because the object is moving--potential energy shows because the object is in a certain position in the field. But, heat energy does not show --it is internal to the object. The object is hotter. We now know heat is related to the internal motions of the constituents that make up the object. The constituents of the object have an increase in kinetic energy which shows up as a higher temperature of the object.
An example of where energy apparently disappears, is when two identical objects collide, as before, but stick together after collision. The law of conservation of momentum tells us that the stuck-together objects must move off with speed v/2 in order that the momentum after collision, namely 2×m×v/2 , is the same as the momentum before, namely, m×v .
The kinetic energy before collision is m×v2/2 whereas after collision it is (2×m)×(v/2)2/2 since the mass of the outgoing object is 2×m and its speed is v/2 . (Remember kinetic energy is the mass multiplied by the velocity squared all divided by two.) If you simplify this expression for the energy after collision you see that it is m×v2/4 , only half of what it was before collision. It would seem that energy had disappeared. We call this kind of collision an inelastic collision which just means one in which the total of the potential and kinetic energies is not conserved. These two kinds of energy are called mechanical energy. I said that it was found that, when mechanical energy disappeared, heat appeared. This was discovered by Joule; he found the exact relationship between the unit for measuring mechanical energy and the unit for measuring heat, the calorie. We now call the unit for measuring any kind of energy after Joule.
Joule's discovering where energy disappeared to in an inelastic collision was very important and made scientists believe that the law of conservation of energy was very fundamental. Since it is merely a restatement of some of the information in Newton's laws of motion, we would expect that it holds as long as Newton's laws hold. But, I guess they forgot about Newton and began to put their trust in energy conservation. The reason that energy conservation includes heat energy is that if you look microscopically at the collision it is not between two objects but between two systems of particles which are moving about randomly as well as having their centers of mass move along systematically. When we say that object number one moves at speed v , we really mean that the center of mass of the system of particles that we call object one is moving at speed v . The other object is at rest before collision, but its particles are also moving about at random--but their center of mass stays fixed. After collision, each center of mass moves at speed v/2 , but the random motions of each system are intensified. This shows up as heat, but is really mechanical energy of the particles. So, in fact, mechanical energy is conserved, at the microscopic level, even when it seems that it is not when we just look macroscopically.
So we emerge from all this with an alternative way of expressing the information in Newton's laws: as the laws of conservation of momentum and energy. But more than that, scientists found the conservation law form of the information more appealing. It is undoubtedly good to have alternative ways of reasoning about physical situations, but this alone would never have been enough to raise conservation laws to the prominence they now enjoy without metaphysical feelings on the part of scientists. The idea of conservation seems to support the idea of design in the physical world.
I have indicated in the last chapter that Newton's laws do not describe the interactions between electric charges. We need Maxwell's laws of electromagnetism or their information equivalent. Newton is just plain incorrect as far as the interactions between fundamental particles go. Does that mean that the laws of conservation of energy and momentum are also incorrect? The answer is yes, if we stick to the same definitions of momentum and energy. But, if we are willing to change the meanings of the words we can get laws that have the form of the old laws.
I will concentrate first on the law of conservation of energy. The person responsible for manipulating Maxwell's laws of electromagnetism into a conservation of energy law was Poynting. His equation is sometimes called Poynting's theorem--like the work-energy theorem. Poynting defined energy in such a way that it was a property of the fields--electric and magnetic--rather than a property of the charges causing the fields. If the fields were static, that is, not changing with time, the energy just stayed in space wherever there was a field. When the field changed with time because a charge was moving, the energy stored at any position could change and this according to Poynting was accompanied by a flow of energy from one point to another. If an electric charge were oscillating back and forth there would be a flow of energy from it outward into space.
I did not write down Maxwell's equations as I did Newton's equations because they are mathematically more difficult. But remember they are equations that relate the way that the electric and magnetic field components, which describe the electromagnetic field, depend on each other and on the source of the fields, namely, electric charges. The emphasis in Maxwell's equations is the field and when you perform mathematical operations on these equations just as we did on Newton's equations, to get a theorem that can be given an energy interpretation, it is natural that the energy will be associated with the field rather than with the charges. Jammer describes it this way:
[Maxwell and Poynting have shown that] the field is the seat of the energy and matter ceases to be the capricious dictator of physical events. [6]
An earlier energy interpretation which involved only static electric or magnetic fields, found that a valid conservation law could be obtained either by associating the energy with the charges or with the field. But, Poynting's assignment to the fields is necessary in the most general case.
The main thing to realize is that the law of conservation of energy for electromagnetic fields does not contain any information whatsoever not contained in Maxwell's equations. From the point of view of worrying about whether or not the energy conservation law proves the existence of design in nature, the question can be decided by looking at Maxwell's equations.
The fact that energy is an artifact, an invention of man and not a part of nature is made completely explicit in the high school textbook on physical science prepared for non-science students (by PSNS project staff):
Much of the usefulness of the energy concept arises from the fact that, when properly defined, the total energy in the Universe is constant. This statement is so fundamental to man's model of the world about him that it has become known as "the principle of conservation of energy." We will discover that if this principle is to apply to all physical interactions and to all situations whatsoever, it will be necessary to invent a number of different kinds of energy. We will also see the need to invent rules for assigning numerical values to the various forms of energy we invent. These rules will tell us how to compute the values of each kind of energy in terms of the properties of objects under any situation imaginable
The rule for determining this number has already been set for kinetic energy:
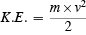
But, we must establish other kinds of energy and give the rules for determining a given amount of each kind if we are going to be able to develop the principle of conservation of energy. That principle is the accounting system of the energies as objects interact with one another. If we assume that energy is conserved in each interaction, then if objects do interact in such a way that the energy of one decreases, the energy of some other must increase. It is possible, of course, for the energies of each of the interacting objects to decrease, but only if they lose energy to the surroundings. Objects can also gain energy from the surroundings.
By this reasoning, we are at liberty to invent as many energies as we wish and in any way we see fit in order to accomplish our objective of producing an energy conservation principle. The principle will only be useful, however, if the number of separate rules necessary to specify all kinds of energy is reasonably small. Generating the law would not be worth the effort if every new phenomenon investigated required a new kind of energy calculated by a new rule. If, however, we can describe all interactions in terms of the exchange of only a few kinds of energy, then the energy conservation principle would provide a new relationship between properties of interacting bodies. Fortunately, it is possible, by identifying only six or eight distinct kinds of energy, to arrive at a principle which turns out to be enormously powerful as an aid in thinking about how bodies interact. Once we are persuaded we have established a principle that is valid for all events, we can use it with confidence to predict what results we shall obtain from experiments we have not yet performed. [7]
From this you can see that my point of view about energy is completely orthodox--but I am not sure that it is the view held by most scientists. It is certainly not the view held by the general public, particularly when the words "energy crisis" are on everyone's lips. Energy becomes more than a concept when we think of running out of fossil fuels.
If you take the scientific view, energy is always conserved--it can neither be "destroyed nor created" as is often said. Why are we constantly being told to conserve energy? The reason is that some things that we assign energy to are more useful than others as a source of energy. It is easier to transfer energy from oil to a motor car to accelerate it than to transfer energy from air. The energy from oil is more available. When we lose energy from our houses to the air we say it is dissipated--it is not concentrated in a way that keeps our bodies warm. That is why we insulate our houses--to prevent the transfer. There are different classes of energy. High class energy, like that assigned to oil or to the heat in a warm house, is more useful. We call energy that is dissipated by nuclear power plants into the lake water used to cool them "thermal pollution." The energy is unwanted.
There is no doubt that the concept of energy is a very good way to describe the changes that are occurring around us but we must constantly remember its roots as an invention of man--as the PSNS book says:
Energy itself is a creation of the human mind. Our confidence that we can find a small number of simple rules for assigning energies so that the sum of all kinds is constant has established the conservation principle as a basic premise of science. [8]
Conservation laws are a form that we want, and we give meaning to all kinds of things like work, potential energy, kinetic energy, energy density, energy flow, and so on to keep our beloved form. And so far we have been successful. But, the thought that we have a general law of nature is an illusion.
Summary
1. All the ideas expressed in this chapter are orthodox although perhaps not uniformly held by all scientists.


