CHAPTER 6
The Impossibility of Isolation
When we are studying a particular phenomenon in nature, such as the way two objects interact with each other, it is customary to focus attention on the objects, to the exclusion of everything else in the universe. We say that we examine their behavior “in isolation.” What I will argue is that isolation is never in practice achievable. This means that the effect of the rest of the universe must be considered. If it appears to be neglected it shows up, in disguise, some other way.
In this chapter, I will be looking at the laws of motion of objects as proposed in the seventeenth century by Sir Isaac Newton in his famous Principia . My intention is to determine their information content. Newton’s laws mention the term body by which he means an object, or a material thing. Laws in physics should really be restricted to dealing only with fundamental objects if we want to label them as fundamental laws. This is because we believe that, if we know the laws that describe the behavior of the fundamental objects, we can derive all the other laws. In Newton’s time the idea of a fundamental object had not been formed so that, in a sense, Newton’s laws are not fundamental laws. From our present point of view we can think of the entire universe as being made up of three fundamental objects, or particles as we usually call them. These are electrons, protons, and neutrons. There are other particles, but we can neglect them in this model. The protons and neutrons group together to form the nucleus of an atom and the electrons move about this nucleus. Niels Bohr devised a model of the atom which was like a solar system in which the electrons moved in orbits around the nucleus, like planets around the sun. You often see drawings of atoms showing several electrons moving in orbits. The number of electrons moving about the nucleus in an ordinary atom is always the same as the number of protons in the nucleus.
The simplest atom is hydrogen. It has one proton in the nucleus and one electron moving about it. I do not say “moving in orbit” about it because we now know that the Bohr model of the atom is not true. But, we still believe that the electron and proton are there and are interacting with one another. The electron and the proton are electric charges. We say arbitrarily that the electron is a negative charge, and the proton is a positive charge. The magnitude, or size, of their two charges is equal but opposite so that when they are together in an atom their total electrical effect nearly cancels out unless something is close to the atom.
Atoms that are heavier than hydrogen have more protons in the nucleus and, of course, more electrons moving about. There is always the same number of electrons as protons in an atom. In heavier atoms, there are always neutrons in the nucleus as well as the protons. The number of neutrons varies. The atom with eight protons in the nucleus and eight electrons moving about this nucleus is called an oxygen atom. Most oxygen atoms that we find have eight neutrons in the nucleus as well. But, a small percentage—0.205%—have ten neutrons and a smaller percentage—0.038%—have nine. These different kinds of oxygen atoms are called isotopes of oxygen.
In heavy atoms, there are more neutrons than protons in the nuclei of isotopes found in nature. The isotopes we find around now—the naturally occurring ones—are the stable isotopes. The fittest survive. Whenever we create the isotope of an atom whose number of neutrons is far from those which occur naturally, the isotope is unstable and breaks up. We say it is radioactive. We can judge the relative stability of different isotopes of an atom by their relative abundances in nature.
This has been a bit of a diversion, but it is necessary to point out that Newton’s laws do not deal with electrons, protons, and neutrons but bodies made up of complex structures of these fundamental particles. The particles form atoms; the atoms form molecules; and the molecules form solids. The bodies Newton was talking about are solids of various shapes. To keep things somewhat simple we will think of bodies that have a simple shape—spherical like a ball—and bodies that are small enough so that we can think of them as being located all in one place, at a point. We will call these ideal bodies point particles, or just particles. Then our study of the laws of motion will be restricted to particles and the way they interact with one another. We will be looking at what is called particle dynamics. Everything about more complex shapes can be explained in terms of the interaction of the particles that make up the complex shapes.
Now I am ready to bring on Newton’s laws of motion. Here they are:
Law I: Every body perseveres in its state of rest or uniform motion in a straight line unless change in that state is compelled by impressed forces.
Law II: Change of motion is proportional to the force impressed and takes place in the direction of the straight line in which such force is impressed.
Law III: Reaction is always equal and opposite to action; that is, the mutual actions of two bodies upon each other are always equal and directly opposite.
In these laws various terms are introduced: “impressed forces,” “change of motion,” “reaction” and “action”. Really there are only two new concepts—one is force. “Impressed force” is just a force—“action” is a force one body exerts on another—“reaction” is the force the second body exerts on the first. “Change of motion” involves the other new concept, namely, mass. By motion, Newton meant the product of the mass times the velocity. This product is sometimes called momentum. The “change in motion” is the time rate of change of the mass multiplied by the velocity. Since, to Newton, mass was assumed to be a constant independent of how fast the body went, this “change in motion” is just the mass multiplied by the time rate of change of velocity—which is what we call acceleration. The second law is often written as a formula which is
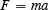
where F is the force acting on a body, m is the mass of the body, and a is the acceleration of the body produced by the “impressed force” F . This formula, as it stands, does not tell the fact that the direction of the acceleration is the same as the direction of the force. This can be indicated by drawing an arrow over both F and a to indicate that the directions are the same.
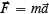
The third law is sometimes written as
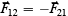
where what is meant by
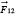 —with the arrow—is the force exerted by particle number
1
on particle number
2
(there are two particles interacting and we label them
1
and
2
). Then
—with the arrow—is the force exerted by particle number
1
on particle number
2
(there are two particles interacting and we label them
1
and
2
). Then
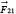 —with the arrow—is the force exerted by particle number
2
on particle number
1
. These two forces are along the same line but point in opposite directions. The minus sign says they are in opposite directions.
—with the arrow—is the force exerted by particle number
2
on particle number
1
. These two forces are along the same line but point in opposite directions. The minus sign says they are in opposite directions.
I am going to look now at the information content of these laws. Newton tried to define the concepts of mass and force independently of the laws, but failed. For example, he said that the mass of a body was its volume multiplied by its density. He then defined density as the mass per unit volume, which is a complete circle. His definition of force basically said it was the cause of acceleration which is said in the laws. So Newton’s three laws must provide a definition of mass and force, concepts that Newton introduced, as well as have some other content.
I have often argued in an elementary class of university physics students that the physical content of Newton’s three laws of motion is zero. Here is the argument: Law I is a special case of Law II since it says that if there is no force there is no acceleration. (Remember Law II says that the acceleration is proportional to the force.) So we can eliminate Law I since it adds nothing not given in Law II. Laws II and III are required to define mass and force. If we use the two-body interaction case, Law II says that:
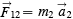
and
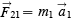
Then using Law III we get:
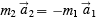
I can write this last equation as:
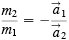
This then defines the ratio of the masses of the two particles as the inverse of the ratio of their accelerations when they interact. Force can be defined by taking this mass and returning to Law II
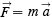
Since now the mass is known—relative to some standard of mass—acceleration can be measured and force calculated. And so we have absolutely no physical content to the laws! Or do we? Mach, in his Science of Mechanics , analyzes Newton’s laws at length and comes to this conclusion:
… its main result will be found to be the perception, that bodies mutually determine in each other accelerations dependent on definite spatial and material circumstances and that there are masses. In reality, only one great fact was established… Different pairs of bodies determine, independently of each other, and mutually in themselves pairs of accelerations, whose terms exhibit a constant ratio, the criterion and characteristic of each pair. [1]
Mach puts his finger on one piece of physical content when he says “pairs of accelerations whose terms exhibit a constant ratio, the criterion and characteristic of each pair.” This gives mass, as defined this way, a physical meaning because the ratio of acceleration is “constant”. Constant over what range of circumstances? One circumstance is that no matter how far apart the interacting bodies are, the ratio is the same. For all interactions the actual size of each acceleration decreases as the bodies get farther apart—but the ratio stays the same. The accelerations get smaller in proportion to each other. Another circumstance is that it does not matter how the bodies are moving when they interact. The ratio of accelerations does not depend on the velocities of the bodies. So the concept of mass is one that is velocity independent since its value, as measured by comparing it with another body, does not depend on the velocities of the bodies.
Because the ratio of accelerations is the same no matter how far apart the bodies are, we can get more information: that the interaction seems instantaneous. It does not take any time at all for the effect of a change in position of body 2 to be felt at body 1 , and vice versa. The acceleration of each body changes instantaneously so as to keep the ratio constant.
So let me summarize the information content we have so far. When two bodies interact, each is accelerated and the ratio of the two accelerations is a constant no matter how far apart they are and what their velocities are at the time of the interaction—interaction being instantaneous. We use this constant ratio to assign to each body a mass, a property of the body which is independent of its motion. If the bodies are particles, the accelerations are along the line joining the particles and point in opposite directions. This means that particles either attract each other or repel each other. (All this last information comes from the fact that the ratio a₂/a₁ is a constant.) We seem to be getting more information content now. Is this all? Newton had a second concept in addition to mass, namely force, and he had arranged his definition of force so that the forces of two bodies on each other were equal and opposite. This appealed to Newton. Here is a passage from his Rules of Reasoning section of the Principia :
We are certainly not to relinquish the evidence of experiments for the sake of dreams and vain fictions of our own devising; nor are we to recede from the analogy of Nature, which is wont to be simple and always consonant to itself. Nature does nothing in vain, and more is in vain when less will serve; for Nature is pleased with simplicity, and affects not the pomp of superfluous causes. [2]
As far as I am concerned the concept of force is superfluous, but Newton’s passion for simplicity in Nature overcame his feeling that “Nature does nothing in vain.” If we do allow concepts in addition to what we really need we must label them clearly as artifacts—man-made, not natural. Let us not admire Nature for its simplicity when it is our own—Newton’s—creation.
There is a simplicity here though in that the accelerations are oppositely directed along a line joining the particles and have a constant ratio. It is here “explained” by the fact that the particles have a property called mass. But is that an adequate explanation of this simplicity? As I mentioned earlier in the chapter, the fundamental particles that interact are the electron, proton, and neutron. The proton and neutron interact only if they are at close range as they are in the nucleus, and the interactions which Newton was talking about do not in any way involve this close-range nuclear interaction. The electron and the proton interact with each other at any distance so it is this fundamental interaction that accounts for many Newtonian interactions. (I leave gravitational interaction aside here.) The interaction between the electron and the proton, or between two electrons, or two protons is not correctly described by Newton’s laws. It is not instantaneous—the accelerations do not have a constant ratio—are not always oppositely directed along a line and are not independent of the velocity of the interacting particles. I will be looking at this interaction in the chapter dealing with electromagnetic interaction but, for the moment, what about Newton? We know his laws do not apply to the fundamental interaction—what, beside gravitational interaction, do they apply to? They apply to large-scale objects pushing and pulling each other in contact with one another. What is more, they are adequate in describing this behavior so that engineers can build cars, airplanes, and bridges. But, they are not information about the behavior of the fundamental particles and thus can be ignored completely as far as additional information content is concerned. This is because we will be able to explain why Newton’s laws hold for large scale objects once we have the proper laws for fundamental interactions. We need only worry about accounting for the laws of the fundamental interactions.
But wait! Not so fast! There is more content lurking around. Mach includes it when he says that “different bodies determine independently of each other and mutually in themselves pairs of accelerations.” This fact, that the interaction between any two bodies is independent of the presence of other bodies that might be interacting with them, is called the principle of superposition. The principle of superposition is a law which says that the effects of a number of different bodies are just superimposed one on top of the other. They do not interfere with the interactions of one another. The final acceleration that any one body experiences is the resultant of the individual accelerations produced by all other bodies present, each acceleration being computed just as if there were no other bodies there.
The principle of superposition does contain information. It is a basic part of the theory of the interaction between fundamental particles, whereas Newton’s laws are not. The principle of superposition was not mentioned directly by Newton; what he did speak about is how the forces are added if more than one force acts on a body. Force has a magnitude and direction—as does acceleration—and thus two forces pointing in different directions are not just added like 2 and 2 to make 4 . In fact, if equal forces are in opposite directions, they add to zero. If they are at right angles, we can represent them as two sides of a rectangle and the resultant is the diagonal of the rectangle starting from the point of application of the forces. In general, any two forces define a parallelogram of forces. Many of you will know all about how to compute the resultant of quantities like forces or acceleration that have magnitude and direction. Such quantities are called vector quantities. We talk about adding vectors.
All this brings me to the most exciting part, the law we threw away so casually—Law I. The first law has the most fundamental piece of information of all. Here is the law again:
Law I: Every body perseveres in its state of rest or uniform motion in a straight line unless change in that state is compelled by impressed forces.
We know that impressed forces come from other bodies so that we can say that a body will continue to be at rest or move in a straight line at a uniform speed if it is isolated from other bodies which might exert forces on it—cause accelerations. The body must be alone in space. Mach calls our attention to a little problem here:
When we say that a body K alters its direction and velocity solely through the influence of another body K´, we have asserted a conception that it is impossible to come at unless other bodies A,B,C… are present with reference to which the motion of the body K has been estimated… If now we suddenly neglect A,B,C… and attempt to speak of the deportment of body K in absolute space, we implicate ourselves in a twofold error. In the first place, we cannot know how K would act in the absence of A,B,C… ; and in the second place every means would be wanting of forming a judgment of the behavior of K… [3]
If the body were alone in space we could not tell whether or not its motion were uniform, or accelerated, or if it were standing still. We need other bodies to provide a background against which motion can be measured. We sometimes say that these other background bodies are a frame of reference for making measurements of position. What Mach says is that our error is twofold in neglecting reference bodies. Beside making measurement impossible, we are presuming that the body K under observation would behave the same way with and without the reference bodies. When we make measurements of the motion of a system of bodies that we claim are isolated, they are not isolated at all—isolation is an impossibility. We have the rest of the universe present, and we can never know how a body would behave if the rest of the universe were not present.
When there are no other bodies near a body that we intend to observe, Newton says that the body will be in either of two states: resting or moving at constant speed in a straight line. Either of these two states is a natural state for a body. We can reasonably assume that these two states are equivalent as far as the body is concerned. The information content of this is that the effect of the rest of the universe on a body is identical in these two states. Suppose that we have a frame of reference and in that frame a body is moving at a constant speed. Now imagine that we are on the body and have another frame of reference moving with the body. We would say that the universe was equivalent to us at rest in the moving frame of reference to what it is to a body at rest in the original frame.
A frame of reference in which a body, uninfluenced by any nearby bodies, is at rest—or moving uniformly—is called an inertial frame of reference. Any frame of reference moving at constant velocity relative to an inertial frame is also an inertial frame. In an inertial frame, a body can maintain a resting position.
All this is well-accepted material. Newton knew about it. He wrote down what has become called his principle of relativity. Here it is:
The motions of bodies included in a given space are the same among themselves whether that space is at rest or moves uniformly forward in a straight line. [4]
The space referred to here is an inertial space. I will call it an inertial environment. I believe, like Mach, that an inertial environment is more than a background against which measurements can be made. Bridgman says this:
We do not have a simple event A causally connected with a simple event B, but the whole background of the system in which the events occur is included in the concept, and is a vital part of it. [5]
The theory of special relativity is based on the Einstein principle of relativity: that the laws of physics are invariant—the same—from one inertial frame of reference to another. This is usually taken to indicate that inertial frames are equivalent but what does that mean? There must be some effect on the particle in an inertial environment that is very definite and different from a particle “isolated” in an accelerated frame. When a particle is all by itself in an accelerated—non-inertial—frame, it will accelerate just as if there were some other particle causing it to accelerate. But, there is no other particle. Its environment at rest in this accelerated frame must be different in the same way as it is different when another body acts on it in an inertial frame, because in both cases it accelerates.
If we presume that the particle accelerating in the non-inertial frame is in its natural state we would assume that it had achieved an inertial environment. Newton’s First Law says that the inertial environment is the natural state of the particle. Is it not reasonable to assume that a particle will always move in such a way as to achieve an inertial environment? This would mean that in an inertial frame the combination of the environment produced by a body that is influencing our observed body and the environment experienced by it accelerating in the inertial frame superimpose to make an inertial environment. The particle accelerating in this way would be in its natural state.
Newton’s laws could then be summed up by saying that bodies behave in such a way as to maintain an inertial environment for themselves. In this point of view, the rest of the universe is not inert or benign. How could it be if a particle in a frame accelerating with respect to the universe cannot remain at rest without holding it at rest? But, normally we just ignore the universe and pretend the particle is isolated. One of the reasons for neglecting the effect of the universe is that most people believe in the idea of laws as part of a grand design—and the law of the equivalence of inertial frames seems eminently suitable.
Sir Fred Hoyle says this in an article on The Future of Physics and Astronomy :
There is also a second reason for the astronomer not to remain idle: the universe, in the large, may be relevant to physics. The current and conventional point of view is that, while the universe may set boundary conditions for the operation of the physical laws, the laws themselves are independent of large-scale structure and could, in principle, be determined by entirely local experiments. The opposite, unorthodox point of view argues that the physical laws as we discover them in the laboratory already involve the influence of the universe as a whole… There are two clues indicating that the unorthodox, nonlocal point of view may be correct. The first is that by taking account of an influence of the universe it is possible to avoid the assumption that the local laws of physics are lopsided with respect to time… The second clue comes in a somewhat roundabout way, from considering particle masses to arise from interactions with other particles. [6]
The point that Hoyle makes regarding “the local laws of physics being lopsided with respect to time” makes reference to the fact that when we have large numbers of particles—atoms—interacting with each other as we have in gas contained in a box, there is an irreversible nature to their behavior. They always move from a more orderly to a more disorderly state, never the reverse. Bridgman speaks about this too:
What prevents the following out through all future time of a definite sequence is the walls [of the box], the atoms of which are supposed to be in such a complex state of motion because they are in connection with the entire outer universe and to a certain extent reflect its complexities, that no resultant regularities are to be expected in the motion which the atoms of the wall impress on the atoms of the gas. [7]
As his second clue Hoyle believes that the masses of the fundamental particles may also be connected with their interactions with the other particles in the universe. I am trying to convince you that an inertial environment is not empty. It is the natural environment of particles. If a particle moves in a straight line at a constant speed relative to an inertial environment what it perceives is an inertial environment. This is a property of whatever produces the inertial environment, which I say is the universe. It indicates that the effect of universe is the same when we move in different directions. There is no special frame that we can say is really “the” frame or “absolute space” as Newton called it. Many frames are equivalent. This is a fact about the universe, not a law governing the universe. Heisenberg hints at this active rather than passive nature of the inertial environment—space—here:
From our modern point of view we would say that the empty space between the atoms in the philosophy of Democritus [the void] was not nothing; it was the carrier for geometry and kinematics, making possible the various arrangements and movements of atoms. [8]
By examining Newton’s laws of motion, I have come to the conclusion that the behavior of particles of matter is determined by their environment. Their natural state is to be in an inertial environment. In an inertial frame, that is, one in which a particle at rest experiences an inertial environment, a particle moving at constant speed in a straight line is also in a natural state. This means that a frame of reference moving at constant velocity relative to an inertial frame is also an inertial frame. In it, the moving particle of the original frame could be at rest. This leads to the principle of relativity which Newton stated and which was the basis of Einstein’s theory of special relativity: that inertial frames were all equivalent to each other as environments for the interactions between any two bodies. As well, there is no one inertial frame that has a superior status to the others. This is stated by saying that there is no such thing as absolute space. There are an infinite number of equivalent inertial spaces. The environment in these spaces is produced, I believe, by all the matter in the universe. As Heisenberg says it is “not nothing,” as space is often perceived to be, but it is “the carrier for geometry [measurements of distance and direction] and kinematics [measurements of motion which include distance, direction, and time].” Heisenberg goes on to say that “this [space] makes possible the various arrangements and movements of atoms” meaning that, without the environment, the atoms would not be what they are. So the examination of the information content in Newton’s laws leads me to focus attention on empty space . The main point of this chapter is to get you interested in things that might be overlooked. I have maintained that the idea of an isolated body is never achievable so can be of no interest to us. But, the environment produced by the universe should be thought about very carefully.
Mario Bunge in his book on Causality and Modern Science has quite a bit to say about the assumption of isolation:
The isolation of a system from its surroundings, of a thing or process from its context … are indispensable not only for the applicability of causal ideas but for any research, whether empirical or theoretical… Analysis is the sole known method of attaining a rational understanding of the whole: first it is decomposed into artificially isolated elements, then an attempt is made to synthesize the components. The best grasp of reality is not obtained by respecting fiction but by vexing fact and controlling fiction … perfect isolation is a theoretical fiction. [9]
Bunge points out that the uncertainties in quantum mechanics have been considered by some thinkers to be “a result of external perturbations, that is, as a consequence of imperfect isolation.” But Bunge adds “However, inertial motion goes of itself in complete isolation and in the absence of causes.” I, following Mach, maintain that an inertial environment is not one of “complete isolation”.
Summary
1. The environment of any body is produced by the other bodies in the universe. (Mach)
2. The natural state of a body is for it to be in an inertial environment.
3. A body will move relative to a frame of reference in such a way as to achieve an inertial environment.
4. In an accelerating—non-inertial—frame of reference a body, which does not have other bodies nearby, will accelerate. It thereby achieves an inertial environment. Acceleration in any frame changes the environment experienced by the body.
5. If a body is in an otherwise inertial environment—in an inertial frame of reference—but is influenced by another nearby body, it will accelerate either towards or away from that body. Its total environment will thereby become an inertial environment.
6. Moving uniformly in an inertial frame does not change the environment of a body from what it is when at rest. This means that the effect of the remainder of the universe is equivalent in the two states.
7. Because there are many equivalent inertial frames, learning about the behavior of objects in one inertial frame gives us information that is useful in many such frames. The information has generality.


