CHAPTER 10
The Stochastic Atom
At the end of the last chapter I suggested that we might think of particles of matter like electrons and protons as undergoing a random, jittery, zigzag, Brownian motion just as a spore or smoke particle can be observed to execute when you look at it under a microscope. This seems reasonable because a relationship between the uncertainties of position and momentum exists in both cases. In this chapter, I will describe a model of the atom called the stochastic atom in which the electron moves about the proton in a Brownian-like way.
Brownian motion has played a very interesting role in physics. The theory of Brownian motion was developed by Einstein. He showed that the average energy of the Brownian particles was the same as the average energy of the atoms of the gas that was causing the motion. Mach was convinced finally by the theory of Brownian motion that atoms did exist. For many years he had thought that atomic theory was nonsense and said so many times:
However, well-fitted atomic theories may be to reproduce certain groups of facts, the physical inquirer who has lain to heart Newton’s rules will only admit those theories as provisional helps, and will strive to attain, in some more natural way, a satisfactory substitute. [1]
It seems rather strange that Brownian motion finally won Mach over to the idea of the reality of atoms and has led me to doubt wave-particle duality. But, I have been unsatisfied for many years with quantum theory and have longed for some more natural substitute. I do not seem to be alone in wanting to explain quantum theory in a less mystical way than invoking a dual wave-particle nature to matter and radiation. Bridgman says this:
There is a sense in which all the revolutionary aspects of quantum theory can be subsumed under the single point of view that the operation of isolation always fails eventually. [2]
Bridgman finds quantum mechanics “revolutionary” and suggests that environmental influences might explain everything much more simply. Others find that the wave-particle dual nature of matter and radiation point of view is very natural and satisfying. Feynman says:
One of the consequences [of quantum mechanics] is that things which we used to consider as waves also behave like particles, and particles behave like waves; in fact everything behaves the same way. [3]
Feynman rejoices in this unity of nature. Wave-particle duality to him accords with the idea of design in the universe. But, I am set against this point of view and must explain the facts in a way that does not imply design.
Before the wave-particle duality of matter and the uncertainty principle were introduced in the 1920’s, Niels Bohr had devised a model of the hydrogen atom in an attempt to explain the spectrum of light which hydrogen gas produces when it is excited. The spectrum of hydrogen consists of a series of lines of different colors rather than the continuous spectrum you get from the sun’s light. This means that the hydrogen atom is producing light of a number of discrete frequencies. In Bohr’s model, an electron moved in orbit around a proton which was the nucleus of the hydrogen atom in much the same way as the earth moves in orbit around the sun. The big difference is that it is an electric attraction between the electron and proton rather than a gravitational attraction as it is with the earth and sun. As I said, the spectrum of hydrogen consists of a number of particular frequencies of light. Bohr said that these were produced by the electron first being given energy, and thus excited to move in an orbit farther away from the proton, then eventually jumping back to the original orbit where it normally moved—the ground state. The different spectral frequencies corresponded to jumps between different possible excited orbits and the ground state
Bohr had a formula for prescribing exactly where the excited orbits might be. It was called a quantum rule. The permitted orbits were called “stationary” states because they were believed to be semi-stable. The electron would stay in an excited orbit for some little time before it jumped to some other “stationary” state or to the ground state. The ground state was truly stable. The frequency f of radiation emitted when the electron jumped from an orbit of energy E2 to an orbit of lower energy E1 he gave by what became called Bohr’s frequency condition
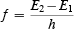
Here, the constant h is Planck’s constant. Planck’s constant had been introduced into physics a decade before Bohr’s work. Remember—Planck and Einstein said that a quantum of electromagnetic radiation of frequency f has an energy equal to h times f . If we rewrite Bohr’s frequency condition as
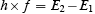
We can interpret it as a statement that energy is conserved in what Bohr called a quantum jump. The equation says the energy of the quantum of radiation ( h×f ) given out is equal to the change in energy of the electron as it moves from orbit 2 to orbit 1 .Here are Bohr’s own words:
1. That energy radiation is not emitted (or absorbed) in the continuous way assumed in the ordinary electrodynamics, but only during the passing of the systems between different ‘stationary’ states.
2. That the dynamical equilibrium of the system in the stationary state is governed by the ordinary laws of mechanics while these laws do not hold for the passing of the systems between the different stationary states. [4]
Although the Bohr theory has now been discarded completely as being wrong, the Bohr frequency condition with its energy interpretation is maintained. I call this Bohr’s “legacy.”
I believe that the second law of thermodynamics says that microscopic conservation of energy is not possible so I must reject the interpretation of Bohr’s frequency condition as an expression of microscopic energy conservation. How can I do it? I must say that I believe that radiation quanta are artifacts and have absolutely no correspondence with reality. I do not believe that it is appropriate to say that h×f is the energy of a quantum of radiation.
There has been, from the beginning, something very wrong about Bohr’s original idea that radiation only emerges when the electron jumps from one allowed orbit to another allowed orbit. According to electromagnetic theory, an electron in an orbit should radiate at a frequency equal to the frequency of the motion in orbit. L.I. Schiff in his book Quantum Mechanics notes the contradiction in Bohr’s theory:
It was difficult to understand why the electrostatic interaction between a hydrogen nucleus [in a Bohr atom] and an electron should be effective when the ability of the accelerated electron [in orbit] to emit electromagnetic radiation disappeared in a stationary state. [5]
Bohr wanted electrostatic interaction to hold the electron in orbit but, he did not want the radiation field due to its acceleration in orbit. He just said baldly that an electron in a stationary orbit did not radiate. The argument went: If it did radiate it would lose energy and gradually spiral into the nucleus and collapse. So scientists became convinced that atoms would all collapse if they did radiate all the time.
Well, the Bohr picture of the atom was discarded when the new wave-particle uncertainty view appeared. The idea of orbital motion keeping the electron from moving right into the proton was abandoned. The present picture of the atom is much vaguer. Here is Feynman speaking of the current view:
What keeps the electrons [in an atom] from simply falling in [to the nucleus]? This principle [the uncertainty principle]… We cannot know where they [the electrons] are and how fast they are moving, so they must be continually wiggling in there! [6]
This explanation says that atoms do not collapse because of a principle —really! Even Feynman is not convinced and ends by saying “they must be continually wiggling in there.” Why do they wiggle? Two answers—They are born wigglers, or, they are being buffeted about. Take your pick—I pick the latter. As you might expect I am not alone in this choice. David Bohm says this:
Indeed, a rather similar behaviour [to an electron in an atom] is obtained in classical Brownian motion of a particle [like pollen in a container of water] in a gravitational field, where the random motion which tends to carry the particle into all parts of the containers is opposed by the gravitational field, which tends to pull it towards the bottom. In this case, the net effect is to produce a probability distribution [formula], which describes a tendency for the particles to concentrate at the bottom and yet occasionally in their random motions to be thrown up to great heights. [7]
I call the model of the atom which treats the motion of the electron as due to a superposition of the electric attraction of the proton as described classically, and random influences from the rest of the universe, the stochastic atom. It might equally well be called the Brownian motion atom. Stochastic applies to things in which there is a random input, an element of chance. For such an atom, probabilistic or statistical predictions are all that would be possible.
I became interested in this stochastic model of the hydrogen atom a long time ago and thought that I might be able to simulate its behavior on a computer. I remembered how difficult it was to model a planet going around the sun by computer; because the errors—or uncertainties—in the precision with which the calculations were being carried out were not negligible, the orbit precessed. I imagined that if uncertainties or random influences were increased—rather than decreased—the motion would not be like an orbit at all but at least the atom would not collapse.
When I ran the program for the model on the computer I had hoped to find that it would take up stable—or semi-stable—states with various average distances of the electron from the proton just as Bohr’s atom did. I would then be able to predict the frequencies of the radiation spectrum. But no such thing happened. There was no sign of equilibrium—in fact, my atom, instead of collapsing, just got larger and larger. The longer I ran the simulation model, the farther the electron got in its drunken motion from the proton. Failure.
I came again at the whole project after several years in an entirely different way. But let me digress. The quantum mechanical model for the atom which incorporates the uncertainty principle was developed by both Erwin Schrödinger and by Werner Heisenberg. I will concentrate on describing Schrödinger’s approach, which is often called wave mechanics. The two formulations have been shown to be equivalent even though they look very different. In Schrödinger’s model all calculations about the atom are probabilistic and are made by computing a function called the probability amplitude function—sometimes called wave function. Using the probability amplitude function, average values can be calculated for the distance the electron is away from the proton, the energy the electron has, and so on. The probability amplitude functions are found by solving Schrödinger’s equation for them. Since the solutions of the equation were to be interpreted as giving the probability of finding the electron in a particular region around the proton, only certain mathematically possible solutions would make acceptable solutions as far as the probability interpretation was concerned. For one thing, the function had to predict that the electron was somewhere. The total probability, added up over the whole region surrounding the proton, had to be equal to one. That meant it was somewhere. This restriction, placed on all possible solutions, yielded a set of functions which were called proper functions or, in German, eigenfunctions. For each one of these acceptable solutions, the average energy could be calculated and this was found to give a precise value, not a value with any uncertainty about it.
Using these average energy values, which were put into a one to one relationship with Bohr’s orbits, and the Bohr frequency condition, the observed spectrum of hydrogen was predicted—or I should say fitted. Bridgman comments on the naturalness of using probabilistic methods:
It is perhaps not too surprising that particles are so easily treated by probability methods, for having come to the end of the effects of structure we have also come to the end of the possibility of explanation in causal terms. [8]
I do not object to probabilistic laws any more than causal laws as long as they can be shown to record the facts about specific things like the fundamental particles or the universe as a whole. I cannot tolerate general laws that cannot be explained. I had attempted to explain the uncertainty principle, from which Schrödinger’s equation can be derived, by seeing a particle as having, as well as its usual classical electromagnetic interaction with other local particles, a random influence from the rest of the universe that buffets it about in a Brownian-type motion.
There were two problems: Why had my Brownian computer model not shown these special privileged states predicted from Schrödinger’s equation and how could I keep my atom from exploding—rather than collapsing? The solution to my problems lay in rejecting Bohr’s legacy to quantum mechanics, his quantum jumps. But how? Let me again go back a bit.
Niels Bohr was very interested in philosophy and was influenced by the philosopher Hoffding. Feuer indicates Hoffding’s position:
[Hoffding] was affirming that a personal choice was as operative in the ultimate methodological commitments of scientists and in their analogies, as it was among religious philosophers and metaphysicians… Hoffding’s unique contribution to scientific thought was his insistence on the heuristic potentialities of the notion of discontinuities in existence. [9]
You can see how quantum jumps would appeal to Bohr if he shared Hoffding’s enthusiasm for “discontinuities in existence.”Bohr changed scientists’ thinking radically. Hanson describes the difference in his Patterns of Discovery:
Pianistic thinking cannot allow violinistic glissandi: pianos allow a C sharp, or a D, but nothing in between. Classical physics regarded nature as a complicated violin: that is, differential equations were always in place; but we cannot think of the atom thus. [10]
Bohr had introduced discontinuous stationary states of the atom and the idea of jumps from one state to another. When his orbital model of the atom was discarded, his quantum jumps survived. Bohr was quick to embrace the new quantum mechanics of Schrödinger and Heisenberg which incorporated de Broglie’s wave nature of particles and Heisenberg’s uncertainty principle along with his quantum jumps. He led a group in Copenhagen to give quantum mechanics an interpretation which emphasized the duality of nature. This “Copenhagen interpretation” dominated and is generally accepted today. There are a few scientists beside Einstein who question this interpretation of quantum mechanics, among them de Broglie and Bohm.
I myself for many years delighted in the many exciting and mysterious ideas in physics. When Donald Ivey and I were preparing television programs we marvelled at the great material we had at our disposal. Duality and uncertainty have a strong dramatic appeal. So much so that I began to suspect that we, as physicists, were indulging ourselves in a pseudo-religious experience, finding the universe so mysteriously contrived. That is when my real doubts began. I fell out of step with the orthodox view of things.
Heisenberg tells of how he became interested in finding a theory for the atom. He was put off by a textbook illustrator’s view of molecules:
In order to explain further just why one atom of carbon and two atoms of oxygen form one carbonic acid molecule, the artist had given the atom hooks and eyes… To me this seemed wholly senseless, because hooks and eyes are—as I saw it—quite arbitrary forms, which can be chosen in different ways according to their technical usefulness. But, atoms are supposed to be the result of natural laws, and guided by them in forming molecules. [11]
The natural laws—such as the uncertainty principle devised by Heisenberg—to me, need explanation, and that is why I am attracted to a stochastic model of the atom. Nelson, in an article in the Physical Review in 1966, describes such a model:
If we have, for example, a hydrogen atom in the ground state, the electron is in dynamical equilibrium between the random force causing the Brownian motion and the attractive Coulomb [electrostatic] force of the nucleus. Its trajectory is very irregular. Most of the time the electron is near the nucleus, Sometimes it goes farther away, but it always shows a general tendency to move toward the nucleus, and this is true no matter what direction we take for time… the electron has states of dynamical equilibrium at the usual discrete energy levels of the atom. [12]
In the article Nelson shows that a stochastic model leads to the Schrödinger equation but he runs into a little trouble trying to explain the character of the probability function for excited states of the atom. The problem is that the function that describes the probability for position of the electron in any excited state has certain places where it becomes zero. We call these positions nodes in the function. There is a definite probability that the electron will be found on either side of the node but no probability that it will be at the node. How does the electron get from one place to another without passing in between? Here is Nelson struggling with the problem:
For real solutions of the time-independent Schrödinger equation, other than the ground-state solution, the probability functions have nodal surfaces… However, it can be shown that the associated Markoff [stochastic] process is well defined in each such region, and that a particle performing the Markoff process never reaches a nodal surface. [13]
Nelson seems to believe that the particle stays in one or other of the compartments between nodes. The answer the Bohr disciples give is that the electron is not really a particle, it has a dual nature and as such can perform this difficult feat. It is like going from one room to another without passing through the connecting door. But that is nature for you, mysteriously contrived. After all, the electron is not to be considered as a particle. But, look at Schrödinger’s equation and what do we see—the expression for the energy of a particle—not a wave-particle. We use the law of Coulomb to compute the electrostatic energy of position of the electron relative to the proton. Now it is, now it is not a particle!
But that is the beauty of the Copenhagen interpretation—we can have it both ways. Bridgman does not mind:
The celebrated remark of Wm. Bragg that we seem forced to use classical [particle] mechanics on Monday, Wednesday and Friday and wave mechanics on Tuesday, Thursday and Saturday may prove not to be a reductio ad absurdum as it is usually taken to be but an ultimate and necessary procedure. [14]
Although he also says this:
The ultimately important thing about any theory is what it actually does, not what it says it does or what the author thinks it does, for these are often very different things indeed. [15]
Schrödinger’s equation gives the right frequencies of the spectrum of hydrogen but that does not mean that what he or Bohr or anybody says about its interpretation need be accepted. After all, Bohr’s theory of orbits gave the right frequencies for the spectrum too.
I was beginning to suspect that the problem might be that there were no quantized excited states of the atom at all. First, my own computer model did not show any. The Schrödinger probability functions for excited states had nodes and would not square with a real particle—as contrasted with a wave-particle—undergoing a Brownian motion, superimposed on motion under the attraction of the proton. But, how would you get a discrete frequency spectrum without quantized excited states?
I now had the answer. Bohr’s assumption about there being no radiation in the ground state or the atom would collapse was unnecessary. My atom did not collapse in fact, it expanded. I needed some way to keep it from expanding. The atom could radiate. If I went by classical electromagnetic theory, the radiation from the ground state would have all frequencies in it, from the random motion of the electron. That would mean a continuous spectrum of frequencies even from the ground state, presumably for any other state as well. But, no one has ever reported observing such a continuous spectrum. Well not exactly true. We know that all macroscopic bodies radiate a continuous spectrum all the time called blackbody radiation. That is what Planck was studying when he stumbled on the idea for the quantization of energy of oscillators. It would be like looking for a needle in a haystack to find the continuous radiation from the ground state of hydrogen. So I did not worry about supposing that one existed. But, what about the discrete spectrum? Even though I thought that the probability functions for excited stable states did not correspond to anything real and rejected them as not proper functions because they had nodes, I knew that any non-equilibrium state of the system could be expressed mathematically as a combination of these functions.
Wait a minute—this is getting rather complicated. I am trying to explain how a spectrum at discrete frequencies can be produced even though the atom never stays in any one of the excited stationary states. First of all let me be clear about what I expect the atom to do. In the ground state it will radiate a continuous spectrum—all frequencies more or less all the time. The motion of the electron is a complex zigzag motion which mathematically is analyzable as the sum of oscillations of every frequency. When the electron in the atom is given additional energy, by being bumped for example, the atom is excited. It has more energy than it has in the ground state. Its motion is similar to what it is in the ground state, and it gradually loses energy and returns to the ground state. In the process, it produces a continuous spectrum as it does in the ground state, but in addition it produces the discrete frequency spectrum. The electron does not necessarily oscillate at these discrete frequencies, but its motion is analyzable as the sum of oscillations at these frequencies.
Perhaps an analogy here would be helpful. I quoted Hanson earlier in the chapter as saying that “Classical physics regarded nature as a complicated violin … but we cannot think of the atom thus…” . There is a sense in which we can relate a violin to an atom. If we keep our finger off a violin string and bow it carefully it will produce a particular discrete frequency just the way one of the strings of a piano does when it is struck. This frequency is produced by the vibration of the string. The two ends of the string are held fixed, and the center part moves back and forth. We say there is a node at each end and a loop at the center. The wavelength associated with this frequency is twice the length of the string. This is one mode of vibration for the string. It is the fundamental mode. But, the mathematical equation which describes the vibrating string has other solutions—other modes of vibration. One such mode has a node in the center as well as at each end. This mode of vibration has a frequency which is exactly twice the frequency of the fundamental mode. We call it the first harmonic of the fundamental. All the modes of vibration that are solutions of the mathematical equation have frequencies that are integral multiples of the fundamental. We call them the normal modes of vibration of the string. But that does not mean that they are the only ways that the string can vibrate. Most of the time it vibrates in a more complicated way, but the more complicated vibration can always be analyzed as a sum of the normal modes of vibration. We get a mixture of the fundamental and its harmonics. Just as a prism separates light vibrations which are a mixture of different frequencies into the spectrum showing the different lines, the ear of a listener can separate the complex sound vibrations into the different frequencies. We can hear the fundamental and the harmonics. The ground state of the violin string is no vibration at all—in the atom there is perpetual motion.
I hope this analogy will help you understand how a discrete spectrum at frequencies predicted by Schrödinger’s equation might exist for hydrogen. In any non-stable state, radiation would be expected at all the different possible discrete frequencies as well as a continuous spectrum. The system if excited would produce the whole observed spectrum. The more the atom is excited, the more prominent the radiation at higher frequencies would be.
As the atom is left alone, it returns to the ground state where the discrete frequencies die out. So you see I reject the idea of quantized excited states in an atom with an electron jumping from one to another thereby producing a photon of a discrete frequency on each quantum jump from higher energy state to lower energy state. Even Schrödinger hoped to do away with quantum jumping. At the beginning of quantum mechanics he said:
If all this damned quantum jumping were really here to stay, I should be sorry I ever got involved with quantum theory. [16]
Bohr was quick to disagree with him:
… remember the Einstein derivation of Planck’s [blackbody] radiation law. This derivation demands that the energy of the atom should assume discrete values and change discontinuously from time to time… You can’t seriously be trying to cast doubt on the whole basis of quantum theory! [17]
I will be looking at an explanation of blackbody radiation that does not require quantized energy states in the chapter called The Two-Slit Mystery .
The stochastic model of the atom answers another kind of question— how is it that atoms are so durable. A stochastic atom would be durable because it has adapted to the environment. In fact, it exists because of, not in spite of, the environment with all its random influences. Heisenberg wondered at the great durability of atoms:
… chemical elements displayed in their behavior a degree of stability completely lacking in [classical] mechanical systems. [18]
On large scale systems like planets, the random influences are not significant but as we go to smaller objects they are dominant. The atom works, I believe, by a combination of deterministic influence, of the proton on the electron, and by random influences, of the rest of the universe on it. C.S. Smith says this:
Significant structure is a mixture of perfection and imperfection. [19]
Summary
1. The model of the atom that is consistent with my world view is one called the stochastic atom. (Nelson et al)
2. If microscopic energy conservation is impossible, which I believe is evidenced by the second law of thermodynamics, then the Bohr frequency condition cannot properly be given an energy interpretation.
3. The idea of a quantum of radiation is thus not supported by the line spectrum of atoms.
4. The natural motion of an electron in an atom is perpetual motion due to the fluctuating effect of the rest of the universe. Collapse of the atom is not likely even if the electron is producing electromagnetic radiation in the ground state.
5. Radiation produced by an electron moving in a Brownian-like fashion under the attraction of a proton, as in the stochastic model of the atom, would be a continuous spectrum of radiation in the ground—unexcited—state.
6. This continuous spectrum might not be observed because all macroscopic bodies radiate a continuous spectrum, known as blackbody radiation.
7. If the stochastic atom is a valid model and is described by Schrödinger’s equation, then solutions of the equation which have nodes cannot be proper solutions. A real particle cannot have a probability density function of position which becomes zero between places where it is non-zero.
8. The only stationary state for a stochastic atom is the ground state. This is the only state whose probability density function has no nodes. Although no excited state is stable, every excited state may be described as a combination of the solutions of the Schrödinger equation that possess nodes.
9. The discrete line spectrum of hydrogen can be explained by the fact that excited states are describable as a combination of the solutions of the Schrödinger equation normally considered proper solutions.
10. An excited atom produces radiation which, when analysed by a device such as a prism, should contain both a continuous spectrum and radiation at certain discrete frequencies simultaneously.


