CHAPTER 12
Trapped Inside
In this century, two very startling and revolutionary changes took place in our thinking about the universe. One of these changes is the idea that at the microscopic level there is inherent unpredictability in the behavior of particles. This unpredictability is negligible with macroscopic objects so that for a long time it was not evident that the uncertainties were of any importance. Newton's deterministic mechanics was perfectly adequate to describe the behavior of baseballs and planets. The second revolutionary change was called the theory of relativity and was devised by Albert Einstein in 1905. All Einstein did in his theory of relativity was to accept, as true, Newton's principle of relativity for the interaction between charged particles. I have said that Newton's laws of motion, his mechanics, do not properly describe the interaction between the fundamental charged particles except in the special case where the interacting particles are released from rest and then interact. Newton's laws can be used for the electrostatic interaction. But, the fact that the interaction is not instantaneous means that any mechanics that says that at every instant the forces of the interacting particles on each other are equal and oppositely directed, as Newton's does, cannot possibly be right.
Einstein did not begin directly by trying to develop new laws of motion but instead started to examine the situation by using the principle of relativity as devised by Newton. This principle comes from Newton's first law of motion:
Law I: Every body perseveres in its state of rest or uniform motion in a straight line unless change in that state is compelled by impressed forces.
The important piece of information in the law is that the natural state of a body is either rest or uniform motion. These two states must be equally natural. It was discovered that only certain frames of reference provided an environment in which an uninfluenced body could stay at rest. These were called inertial frames of reference. A frame moving at uniform speed relative to an inertial frame must also be an inertial frame, or Newton's first law would not be true. Newton stated the principle of relativity this way:
The motions of bodies included in a given space are the same among themselves whether that space is at rest or moves uniformly forward in a straight line.
In this statement Newton claimed that it is a fact that the interaction between two bodies is the same in all inertial frames. Of course, Newton thought of the interactions as being the kind he described in his other two laws of motion: instantaneous, and either attractions or repulsions along the line joining the interacting bodies. Einstein stated his principle of relativity by saying that the laws of Physics are invariant from one inertial frame of reference to another. But, to work out the theory, he basically used only one set of laws--Maxwell's laws of electromagnetism. And from these he used only the piece of information that the interaction between charged particles is not instantaneous but retarded. The interaction is straight-line with speed c and independent of the motion of the source particle. Einstein said that, in all inertial frames of reference, the behavior of interacting charges is the same.
The next step in the development is to try to relate observations of a single interaction as made in two different inertial frames. It is easy to appreciate that the position coordinates of objects relative to two different frames will be different. What was not as obvious is that the times of the events as measured in the different frames will be different. Suppose that we are observing two particles; I will speak first of the description of the interaction in frame 1 . To describe the position of an object in a frame, we specify three numbers called coordinates. The frame of reference can be thought of as three rods stuck together so that each is at right angles to the other two, the way the edges of a box come together at a corner. The three rods are called coordinate axes and labelled by the names: x -axis, y -axis, and z -axis. To specify the position of an object relative to this frame, we give the three distances of a trip you take from the point where the rods meet, which we call the origin of coordinates, up to the object. We are describing a trip with three legs, all at right angles to each other. You travel first along the x -axis, then in the x-y plane parallel to the y -axis, then out of the plane in a direction parallel to the z -axis. The three distances are written as (x, y, z) and they describe the position of the object. We must also write the time at which the particle has this position because the times for the two interacting particles will be different; remember the interaction is retarded. So, in frame 1 , particle 1 is at (x1, y1, z1) at time t1 and is being influenced by particle 2 at (x2, y2, z2) at time t2 . The time t2 is earlier than t1 by the amount of time the interaction takes to travel from (x2, y2, z2) to (x1, y1, z1) at speed c . In terms of the coordinates--which by the way, are called Cartesian coordinates after Descartes--the distance d between the two particles is
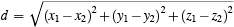
You may know this fact about Cartesian geometry; it is nothing magic. It all comes from Pythagoras' theorem--Remember, the square on the hypotenuse is equal to the sum of the squares on the other two sides of a right-angled triangle. The relationship between the two instants of time is thus
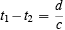
The difference in time is the time required for the interaction to travel the distance d at speed c . Sometimes the coordinates of the particles are written to include the time as a coordinate. We say that particle 1 being at (x1, y1, z1) at time t1 is an event described by the coordinates (x1, y1, z1, t1) . We can call it event 1 . The event 2 is described by (x2, y2, z2, t2) ; this means that particle 2 is at position (x2, y2, z2) at time t2 . In frame 1 , event 2 is influencing event 1 ; we say that there is a causal connection between event 1 and event 2 . (The talk gets quite fancy.)
Now suppose we look at exactly the same two events from frame 2 . We will call their coordinates:
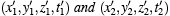
The two events must still be causally connected. This means that
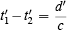
where
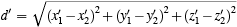
The two basic premises of Einstein's relativity are: first, that a particle moving at constant velocity in one inertial frame of reference, and thus judged to be uninfluenced, will be observed as moving at constant velocity in another; and second: that two events judged as causally connected in one frame will be so judged in another. Nothing whatsoever about either of these two premises is weird. Where do we get the idea that Einstein's relativity is weird? We get it when we try to find the mathematical relationship between the coordinates of an event in one frame, and the coordinates of the same event in another. We find that this relationship, which is called the Lorentz transformation, says that the time t' of an event in frame 2 depends not only on the time t in frame 1 but also the position (x, y, z) of the event in frame 1 . Events that happen at the same time in frame 1 are not assigned the same time in frame 2 , unless they also happen at the same place. This means that we may judge events as simultaneous in frame 1 and find that they are not simultaneous in frame 2 . This leads us to say that time is not absolute; it depends on your frame of reference. This is in conflict with the Newtonian point of view. Here is Newton's statement in the Principia :
I. Absolute, true, and mathematical time, of itself and from its own nature, flows equably without relation to anything external, and by another name is called duration; relative, apparent, and common time, is some sensible and external (whether accurate or unequable) measure of duration.
He went on to say this about space:
II. Absolute space, in its own nature, without relation to anything external, remains always similar and immovable. Relative space is some movable dimension or measure of the absolute space.
You can imagine, if time in frame 2 depends on position as well as time in frame 1 , that position in frame 2 depends on time in frame 1 as well as position. This means that the length of an object depends on the frame. If it is at rest in one frame and has a certain length, in the second frame it will have a different length; it will be measured to be contracted. If two events in frame 1 have a time interval between them and happen at the same place--think of a pendulum bob swinging out and back--the time interval, as measured in frame 2 , will not be the same. It will be longer--we say that the time is dilated. If I call the pendulum swinging in frame 1 a clock, its tick, as judged in frame 2 , will be longer. It appears to be running slow. You have often heard that clocks in moving frames run slow compared to clocks at rest. And what is more, all these effects are relative. If in frame 1 you made measurements on a clock or a distance (a ruler) held fixed in frame 2 , you would say that the clock was running slow and that the ruler was contracted.
Newton's mechanics was based on the idea that the measurement of time and space (distance) was independent of the frame as long as it was inertial. Maxwell used the same notion:
We shall find it more conducive to scientific progress to recognise, with Newton, the ideas of time and space as distinct, at least in thought, from that of the material system whose relations these ideas serve to coordinate. [1]
How did we get to the point of having to mix time and space in a sort of four-dimensional world where we must give (x, y, z, t) instead of (x, y, z) for every event? We got to this point, I believe, because the things we are using to make measurements involve what we are trying to measure. We are trapped inside the universe and cannot stand outside with an independent clock and a ruler and make measurements. Schlegel says this in his book Completeness in Science :
Physically, we come to strong and hitherto unknown limitations on our knowledge of nature when the object of investigation and physical entities by which we study the object become the same. [2]
But, what are we using for a clock or a ruler? Larmor notes this in the appendix to Maxwell's book Matter and Motion :
It is impossible to ignore the rays of light as messengers of direction and duration from all parts of the visible universe. [3]
Rulers must be straight. We use light--or electric interaction--to define straight lines. How do we judge whether or not light--or electric interaction--travels in a straight line? That is the definition of a straight line. That is how we tell if something is straight; by sighting along it or shining a laser along it; light is the messenger of direction. So it is not surprising that electric interaction travels in straight lines. What about the speed of electric interaction--light? Why is it the same in two frames of reference?
Imagine an experiment in one frame to measure the speed of light by timing light as it goes along a ruler from one end to a mirror at the other and back again. I will call this the "speed" ruler. To time it we would need a clock. As a clock let us use another ruler with a mirror at each end. Start a beam of light at one end and say that one tick of the clock is the time it takes the light to go down to the far mirror and back. (Remember a tick must be a motion that comes back to the same place.) Perhaps you can see that if the two rulers are the same length that it takes exactly one tick of the clock for the light to go down and back on the speed ruler. How could it be otherwise, since they are really identical instruments: one for the speed of light experiment, and the second a clock for the measurement of time? With this experimental set up you can easily see that no matter what inertial frame you are in, you get the same value for the speed of light. But is it really the same in all frames? Again, we are trapped. We could never tell whether it was or not.
But, you may say, why not use a different kind of clock? There are no different kinds of clocks. All clocks are basically electromagnetic, with the possible exception of radioactive decay clocks.
So the peculiar results of Einstein's relativity stem from the fact that we assume that, in all inertial frames of reference, light--or electric interaction--travels in straight lines at speed c . We come to recognize that there is no independent clock--or ruler--or else we could tell whether light really travelled in straight lines at constant speed or not. We admit that we are trapped inside with instruments that depend on the thing that we are measuring. We assume light travels at a uniform speed but how do we know? This is Mach on the subject, some time before Einstein formulated his special relativity:
... time is an abstraction, at which we arrive by means of the changes of things... A motion may, with respect to another motion, be uniform. But, the question whether a motion is in itself uniform, is senseless. [4]
As he points out, we judge that light travels at a uniform speed by comparing it with something that we believe travels at a uniform speed--with light of course. Sometimes we say light can never overtake light; it all travels at the same speed. The electric interaction is simple as far as these two facets of it are concerned because they define our universe. They are the basis of all our knowledge, and the basis cannot be independently checked.
It is generally accepted that there is no such thing as time apart from the ticking of clocks and clocks are only judged as good time keepers relative to each other. Feynman says:
... "best" clocks are those which we have reason to believe are accurate because they agree with each other. [5]
I have tried to explain why the speed of electromagnetic interaction is the same in all inertial frames, because that is the really peculiar thing about Einstein's relativity. If you accept the idea of laws of nature you say--How reasonable it is that a law which says the speed of light--electric interaction--is constant, is the same--invariant--in all inertial frames! That is the nature of nature. But if you are, like me, unable to accept the idea of general laws you must ask for an explanation of this fact. Otherwise, it seems like a design feature of the universe. I have not tried to explain in detail about time dilation because it is not central. The Berkeley text on relativity says this:
There is nothing mysterious about clocks. If there is anything mysterious about special relativity, it is the constancy of the speed of light. Granted that, everything else follows directly and fairly simply. [6]
I cannot just grant "the constancy of the speed of light." I must explain it to myself. Then I can see why the speed is invariant from one inertial frame to another. Here is Feuer on the subject:
The logical content of the principle of relativity was indeed an absolutist one, a statement of a principle of invariance. Given the requirement, however, of the conformity of laws of nature to the Lorentz transformation, and the principle of the constancy of the velocity of light, there followed the remarkable consequences of the relativized status of time and spatial distances... The startling relativist consequence rather than the absolutist postulate was what affiliated Einstein's theory emotionally with the relativist school. [7]
It is the "absolutist postulate" that to me must be explained, not all the relativistic consequences. They are easily explained once the invariance of the speed of light--electric interaction--is explained.
So we end up with two facts--first, that as far as fundamental particles alone are concerned one inertial frame is equivalent to another. Second, when two particles interact we just assume that the interaction travels in straight lines at constant--or uniform--speed and take the speed to be, by definition, the same in all inertial frames. In this way, we get distance and time measurements all interwoven with rather bizarre consequences like time dilation and length contraction.
But, Einstein's principle of invariance of the laws of physics from one inertial frame to another is, in itself, a general law. He says all laws are invariant. In order for me to show that it is not a general law but really a specific fact, either about electromagnetic interaction or about the universe, I must be sure that there are no other general laws to which it has been found to apply. It does apply to the wave-particle duality of matter. De Broglie used relativity to derive his wavelength of a particle of matter. I have argued that the uncertainty which gives rise to the appearance of a dual nature of matter can be attributed to a fluctuating influence of the rest of the universe on the particle. I indicated that this produced a Brownian type of motion, in which the product of the uncertainties in position and velocity were characterized by a constant h , Planck's constant.
Einstein's principle of invariance would say that this law is the same from one inertial frame to another and that the constant h would also be the same. This to me must be a fact about the universe--that the inertial effect on a particle is the same in all inertial frames, and that the fluctuating effect is also the same. If it were not a fact, we would be able to distinguish one inertial frame from another on the basis of a quantum mechanical effect. If we assume that the fluctuations are due to the continuous radiation of atoms in their ground states, the Planck blackbody radiation graph can be derived from the fact that the radiation environment is the same from one inertial frame to another. It is, as they say, "Lorentz invariant." This means that the fluctuations are the same in all inertial frames. So the real information content of the blackbody radiation distribution curve is that atoms radiate in the ground state--at absolute zero--and this radiation is the same from one inertial frame to another. This explains why radioactive clocks agree with electromagnetic clocks.
Einstein believed that the laws of physics were invariant from one inertial reference frame to another. Newton's mechanics was not invariant so Einstein discarded it and substituted his own mechanics--relativistic mechanics. To quote myself:
Underlying the principle of relativity is the idea that what happens in a physical situation [say two particles interacting] should not depend on the frame of reference in which the happening is described. This means that the same laws that analyze the behavior of bodies interacting among themselves relative to one inertial frame can be used to analyze their behavior relative to any other inertial frame. For the purpose of analyzing motions one inertial frame is as suitable as another; that is, there is no preferred frame. [8]
What Einstein was doing in producing relativistic mechanics was designing a set of generalities that could be used to analyze interactions in different inertial frames and which would themselves remain the same. One set of laws would be used for all frames. So he set about to find this set of laws. Again quoting myself:
Newton's laws of mechanics are not invariant under the Lorentz transformations. This is most obvious from the fact that the acceleration of an object is not invariant under these transformations. Acceleration [remember F=m×a ] must certainly lose the position on center stage that it had in Newtonian mechanics. Force, mass, and momentum too are quantities that are intimately linked with Newton's laws and, as understood by Newton, cannot be of service. But, Newton's laws had certain features which would be good to perpetuate if possible. For one thing, the ideas of force, mass, momentum and later energy have been built up as strong intuitive notions over the centuries of thinking in Newtonian terms. Another and absolutely invaluable feature is the fact that Newton's laws enabled us to treat a system of interacting bodies as a single entity whose interactions with other such systems could be calculated. In this way we could ignore, if we wanted to, any internal complexities of a system. [9]
This analysis is too involved mathematically to present here, but two of the results are simple enough. We redefine mass so that it is no longer a constant independent of the velocity of a body but is a quantity which increases as velocity increases, approaching infinity as the particle's speed approaches the speed of light. This explains for some people why things cannot travel faster than light. I prefer to think that a charged particle accelerates in response to the presence of another charged particle and that it could not be accelerated to a greater speed than the speed at which the electric action between them travels. How could it be induced to go any faster?
In trying, to obtain conservation laws for relativistic mechanics Einstein found that the laws of conservation of momentum and energy must go as a pair. In Newton's mechanics they were separate. Also, the quantity which would be called energy by Einstein is given by the famous formula
E = mc2
This is sometimes construed as saying that mass can be converted into energy. But, it is no different from the expression for kinetic energy in Newton's mechanics
E = ½mv2
In fact, at low speeds Einstein's formula becomes Newton's formula but with an additional term which is called the rest energy of the particle.
The rest energy is always there since we cannot destroy electrons or protons; so it is not much use. In Einstein's mechanics, the total mass of two interacting particles can be different when they are close from what it is when they are far apart. This sometimes is construed as changing energy to mass. It takes energy to bring them close if they repel, and the mass will be greater together than apart. If they were held together as protons are in the nucleus by an attraction at short range then energy would be available if the attraction were broken. This is what happens in nuclear fission. A neutron entering a uranium nucleus breaks it into pieces which repel each other electromagnetically, and energy is released. There is, in fact, a mass difference between the nucleus and the final pieces that agrees with Einstein's formula ( E=mc2 ) but the energy released does not require relativity to understand. Einstein's mechanics applies equally well to any chemical reaction. In a chemical reaction the amount of energy released in each interaction represents a very small mass equivalent. So we do not notice the difference between the mass before and after the reaction. In chemistry, we use the law of conservation of mass, but it is not precisely correct. The need to use relativistic mechanics is more evident in nuclear reactions. Perhaps that is why we associate Einstein more with nuclear energy than with chemical energy.
There is a law in the list I gave from Constant's book on the Fundamental Laws of Physics that I have been ignoring--besides the law of gravitation--that is the Pauli exclusion principle. The reason I have left it until now is that I needed to have looked at both Schrödinger wave mechanics--quantum mechanics--and the theory of special relativity. Here is a summary of the situation as described in a book Fundamentals of Quantum Mechanics by Persico:
The necessity for this refinement [to use relativistic mechanics rather than classical mechanics for the electron in a hydrogen atom] becomes evident when we consider that the results of Schrödinger wave mechanics are not invariant under a Lorentz transformation.
Another fact which was partly neglected... is the existence of an intrinsic angular momentum (spin) and a magnetic moment both in the electron and in the proton... At first, an attempt was made to deal separately with these two causes of inexactitude of quantum mechanics... Pauli succeeded in introducing the spin hypothesis into (nonrelativistic) quantum mechanics, constructing a remarkable theory... But the most satisfactory solution of both these questions was found by Dirac who showed that the two modifications--the one concerning relativity and the one concerning the spinning electron--are conceptually reduced to one and the same modification... When wave mechanics is given a suitable relativistic form, there follows the existence of the spin and of the magnetic moment, with their correct values and rules... without the necessity of introducing them by an ad hoc hypothesis. From the Dirac theory we may then obtain the Pauli theory as a first nonrelativistic approximation. [10]
From my point of view, the Schrödinger equation is a good representation for the stochastic atom in which the electron and proton are charged particles subject to their mutual electromagnetic interaction and a Brownian motion due to the influence of the rest of the universe. Dirac was able to use relativity, which remember incorporates the finite speed of the interaction between the electron and proton, and produce from Schrödinger's equation the idea of a spinning electron--and proton--with a magnetic moment that he could calculate. Where did it come from? It needs explanation as far as I am concerned. A magnetic moment comes when a charge spins or moves around in a circle. Certainly in the atom the electron is moving about. Its motion is complex, but it can be resolved into a number of basic motions. That is what I believe happens. There is one component that corresponds to a spinning motion, and one corresponding to an orbiting motion as well as the random motion. If the interaction between the electron and proton were instantaneous, there would be no velocity dependent part to the interaction, but it is not instantaneous, so that the velocity dependent part is apparent and is identified as a magnetic interaction. We get spin-orbit interaction and so on. The proton also is not standing still; it is jiggling about and creates a magnetic effect. It has a spin.
The Pauli exclusion principle is used most often to try to understand atoms that are more complex than hydrogen. In a many-electron atom, the electrons repel each other in addition to being attracted to the positive nucleus. We try to understand their behavior in terms of the solutions of the Schrödinger equation for the hydrogen atom. As I said, the Schrödinger equation has stable--non time-dependent--solutions for the ground state and for a series of excited states. Each of these solutions has a set of integers associated with it. These integers are called quantum numbers. When there are a number of electrons in an atom, we say that each one is associated with a hydrogen stable state. We assign quantum numbers to the electrons and Pauli's exclusion principle says that no two electrons can have the same set of quantum numbers. This means that each electron is described by one of the stable excited state wave functions for the hydrogen atom. Here is Feynman:
... in a situation where there are many electrons, it turns out that they try to keep away from each other. If one electron is occupying a certain space, then another does not occupy the same space. More precisely, there are two spin cases, so that two can sit on top of each other, one spinning one way and one the other way. But after that we cannot put any more there. We have to put others in another place, and this is the real reason that matter has strength. [11]
For complex atoms, the probability functions for electrons are built up from hydrogen-like probability functions, and the reason for insisting that only one of a kind must be used is said to be that electrons are all identical. Since, in fact, you cannot keep track of any one electron in order to say it has such and such a probability distribution--with a given set of quantum numbers--it is really just a way of describing the behavior of all electrons present. From my point of view, there cannot be a precise one-to-one correspondence between excited state wave functions and electrons because of the nodes. It is just that, as a group, the set of wave functions represents the set of electrons. Certainly, the Pauli principle has to do with electrons being identical. This fact--that all electrons are identical should be explained. Hanson says this:
It might be objected: No two things are ever perfectly identical. Identical twins can be remarkably similar, but they can always be distinguished ultimately. Two postage stamps, fresh from the same block, will be quite different in detail under a microscope. The finer the scale of observation, the more discrepancies will be found. What is the physicist claiming? That two particles of the same kind are completely alike, with no possible difference between them whatever? Even were they created perfectly identical, could they remain thus? They 'collide' with their neighbours millions of times a second. Would they not become deformed with all this pounding? [12]
I have already suggested that a fundamental particle may constantly be being renewed. That is why they do not become "deformed with all this pounding."
Dirac made the Schrödinger theory relativistic but in the 1950's work was done to show how the quantization of radiation--which I reject--causes certain deviations from Dirac's theory. The theory is called quantum electrodynamics (Q.E.D.). In an article on The Concept of the Photon in 1972 Scully and Sargent indicate that Q.E.D. is necessary to explain certain things:
The quantized field is fundamentally required for accurate description of certain processes involving fluctuations in the electromagnetic field: for example, spontaneous emission, the Lamb shift, the anomalous magnetic moment of the electron, and certain aspects of electromagnetic radiation... Perhaps the greatest triumph of the photon concept to the explanation of the Lamb shift between, for example, the 2S1/2 and 2P1/2 levels in a hydrogenic atom. [13]
According to the relativistic Dirac theory these hydrogen levels have the same energy, in contradiction of the experimentally observed frequency splitting of 1057.8 MHz. We can understand the shift intuitively by picturing the electron forced to fluctuate about its "Dirac" position because of the fluctuating vacuum field. The situation is clearly complicated and I do not pretend to be able to disentangle it. But, there does seem to be room for ambiguity. Quantum electrodynamics is very difficult to understand and is certainly not part of a low-level course in Physics. Some Physicists would swear by it; most do not understand it.
Must our explanation be quite so esoteric?
Summary
1. In an inertial frame, light--electromagnetic interaction--travels in straight lines by definition; light travels at a constant speed by definition. These define distance and time in any inertial frame.
2. The fluctuating effect of the rest of the universe on a particle of matter is the same in all inertial frames.


